こんにちは!現役京大生のむぎといいます!
今回は、確率の最大・最小の問題を攻略していきます!!
確率の最大・最小の問題は、
整数関数の最大最小の分野に属しています
よって今回は整数関数の最大最小について勉強していきます!!
整数関数の最大最小の問題は
このような理由から、とても重要なテーマです!
この記事で得られる学び
この記事を読み切るころには次のような学びが得られているでしょう!
- 整数関数の最大最小問題の基本的な解き方
- 確率の最大最小の解法
- 数列の和の最大最小の解法
- 具体的な2つの解法のステップ
最大最小問題のどこを学ぶの?
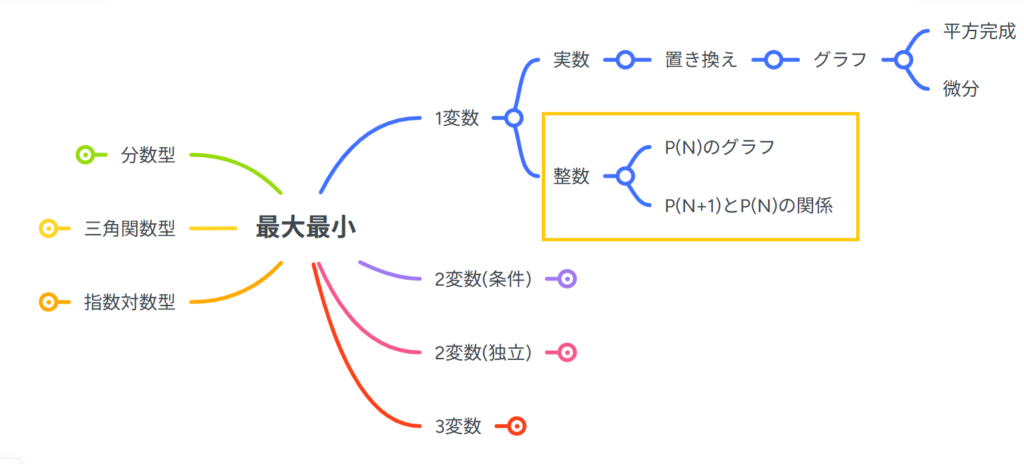
整数関数の最大最小問題の全体での位置です!
全体像を知りたい人はこちらのリンクからどうぞ!
例題
今回の例題です
\(n\;\)を3以上の自然数とする。さいころを振る操作を繰り返し、1の目が3回出たら操作を終了する。\(\;n\;\)回目に操作が終了する確率を\(\;P_n\;\)とするとき、\( \;P_n\; \)が最大となるときの\( \; n\; \)を求めよ。
重要度と難易度
| 重要度 | ★★★☆☆(3) |
| 難易度 | ★★★★☆(4) |
この分野は固有の解き方なので、重要度としては普通くらいです。
しかし、解法を知らないと解くのが難しいので解法は知っておく必要があります。
結構難しい部類の問題ではあると思いますが、わかりやすく解説していきます!!
解法ステップ
整数関数の最大最小問題の解法ステップを解説します!
主な解法は2つです!!
1.\(P(N+1),P(N) \;\)の関係を調べる
- \(\;P(N)\;\) を求める
- 確率問題なら\(\; \frac{P(N+1)}{P(N)}\;\)と1との大小を調べる
- それ以外なら\(P(N+1)-P(N)\)の正負を調べる
2.\(\;P(N)\; \)のグラフを調べる
- \(\;P(N)\;\) を求める
- 関数\(\;f(x)\;\)と捉えて、グラフを書く
- グラフから最大、最小となる整数\(\;N\;\)を見つける

1つ1つ解説していくね
1.P(N+1),P(N) の関係を調べる
1.確率 \(\;P(N)\;\) を求める
\(n\;\)を3以上の自然数とする。さいころを振る操作を繰り返し、1の目が3回出たら操作を終了する。\(\;n\;\)回目に操作が終了する確率を\(\;P_n\;\)とするとき、\( \;P_n\; \)が最大となるときの\( \; n\; \)を求めよ。(例題再掲)
まずは、確率\(\;P_n\;\)を求めます!
今回の問題ではまず
\(\;n-1\;\)回までに1の目がちょうど2回でる
かつ
\(\;n\;\)回目に1の目がでる確率
であるのでまず、\(\;n-1\;\)回までに1の目がちょうど2回でる確率を求めます
今回の問題は、反復試行の問題ですので
を使います
今回の問題に当てはめます
“あること”にあたるものは、”1の目が出ること”であるので
\(\;p\;\) → \(\;\frac{1}{6}\;\)
\(\;n-1\;\)回試行するので
\(\;n\;\) → \(\;n-1\;\)
ちょうど2回起こってほしいので
\(\;k\;\) → 2
こうなります!
よって、\(\;n-1\;\)回までに1の目がちょうど2回でる確率は
\[ P={}_{n-1}C_{2}(\frac{1}{6})^2(\frac{5}{6})^{n-3}\]
次に\(\;n\;\)回目に1の目がでる確率を求めますが
これは普通に\(\;\frac{1}{6}\;\)ですね
求める確率\(\;P_n\;\)は
\(\;n-1\;\)回までに1の目がちょうど2回でる確率かつ\(\;n\;\)回目に1の目がでる確率
よって
\[ P_n={}_{n-1}C_{2}(\frac{1}{6})^2(\frac{5}{6})^{n-3}*\frac{1}{6}\]
2.分数と1との大小を調べる
この手順は、確率問題のときに使うものです!!
\[ \; \frac{P(N+1)}{P(N)}\;\]
として、1との大小を比べます!
この時のポイントを紹介します!!
- \(\;{}_{n}C_{k}\;=\frac{n!}{k!(n – k)!}\)を使う
- 分数にして約分!!
こんだけ!!
\(\;{}_{n}C_{k}\;=\frac{n!}{k!(n – k)!}\)をつかうと
\[ {}_{n-1}C_{2}=\frac{(n-1)!}{2!(n – 3)!}\]
\[ P_n=\frac{(n-1)!}{2!(n – 3)!}(\frac{1}{6})^2(\frac{5}{6})^{n-3}\]
あとはこれを分数にして約分するだけ!
\[ \; \frac{P_{n+1}}{P_n}\;= \frac{\frac{n!}{2!(n – 2)!}(\frac{1}{6})^2(\frac{5}{6})^{n-2}}{\frac{(n-1)!}{2!(n – 3)!}(\frac{1}{6})^2(\frac{5}{6})^{n-3}}\]
\[ \; \frac{P_{n+1}}{P_{n}}\;= \;\;\frac{n}{(n – 2)}\;(\frac{5}{6})\]
難しそうに見えるかもしれませんが
やっていることはとても単純です!
- \(\;{}_{n}C_{k}\;=\frac{n!}{k!(n – k)!}\)を使う
- 分数にして約分!!
そしたら、次は1との大小を比べます!!
\[ \; \frac{P_{n+1}}{P_n}\;= \;\;\frac{n}{(n – 2)}\;(\frac{5}{6})>1\]
となるとき
両辺に \(6(n-2)\) をかけて
\[\;5n>6(n-2)\]
\[\;5n>6n-12\]
\[\;12>n\]
これのイメージを考えてみましょう
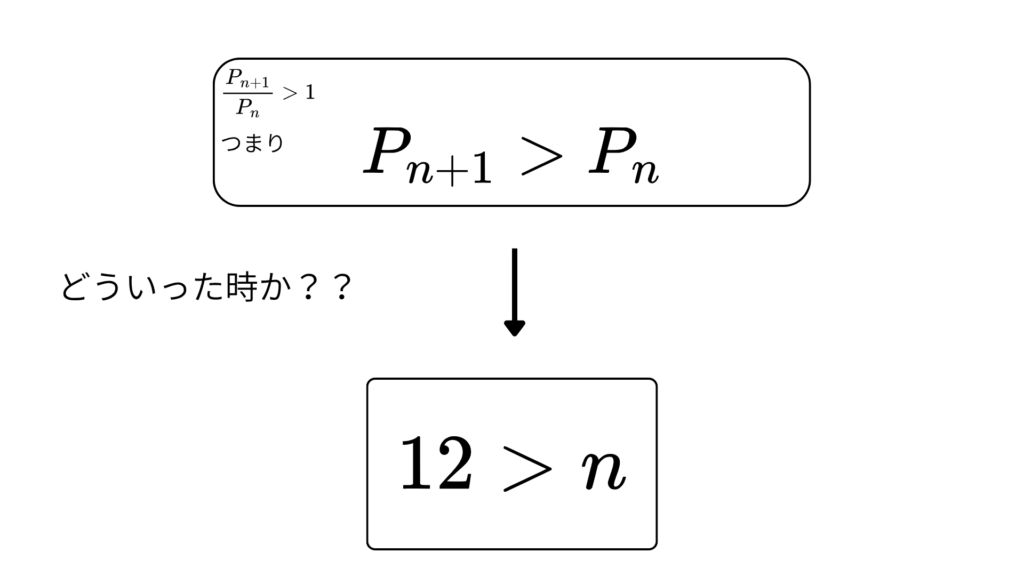
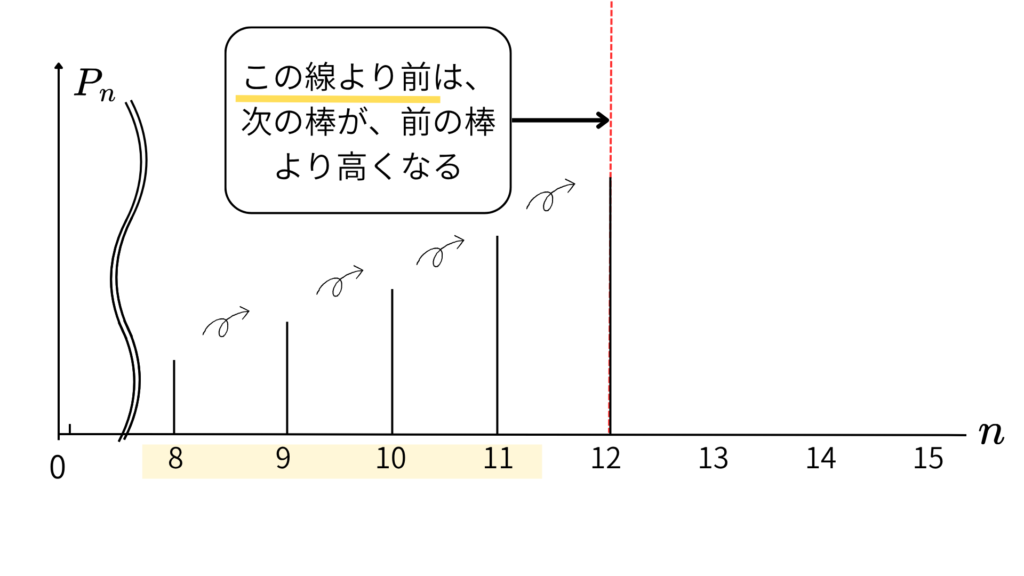
こんな感じですね!
逆に今度
\[ \; \frac{P(N+1)}{P(N)}\;= \;\;\frac{n}{(n – 2)}\;(\frac{5}{6})<1\]
となるとき
両辺に \(6(n-2)\) をかけて
\[\;5n<6(n-2)\]
\[\;5n<6n-12\]
\[\;12<n\]
今度はこのイメージを考えてみましょう!
さっきとは、不等号の向きが逆なのに注意しましょう
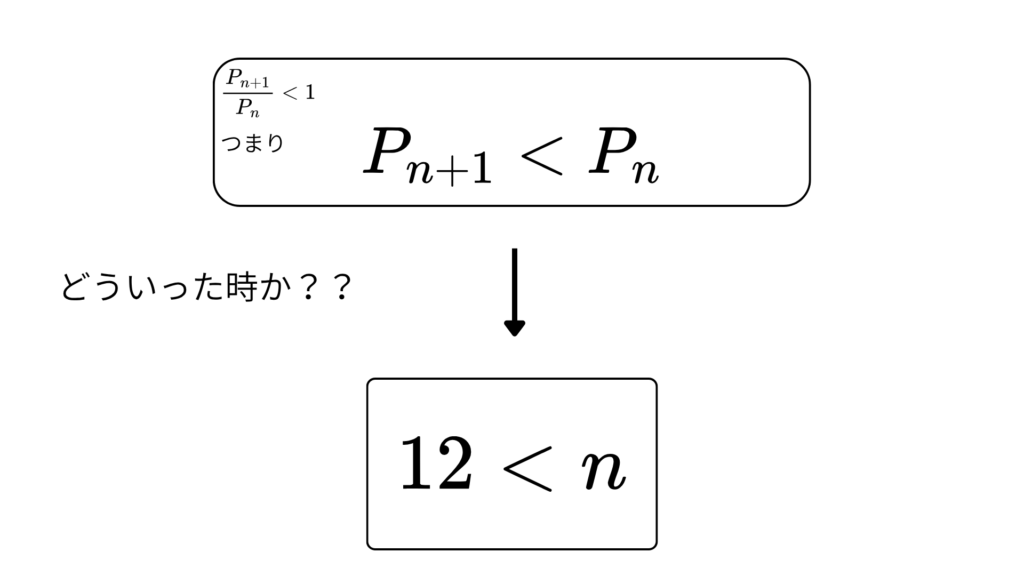
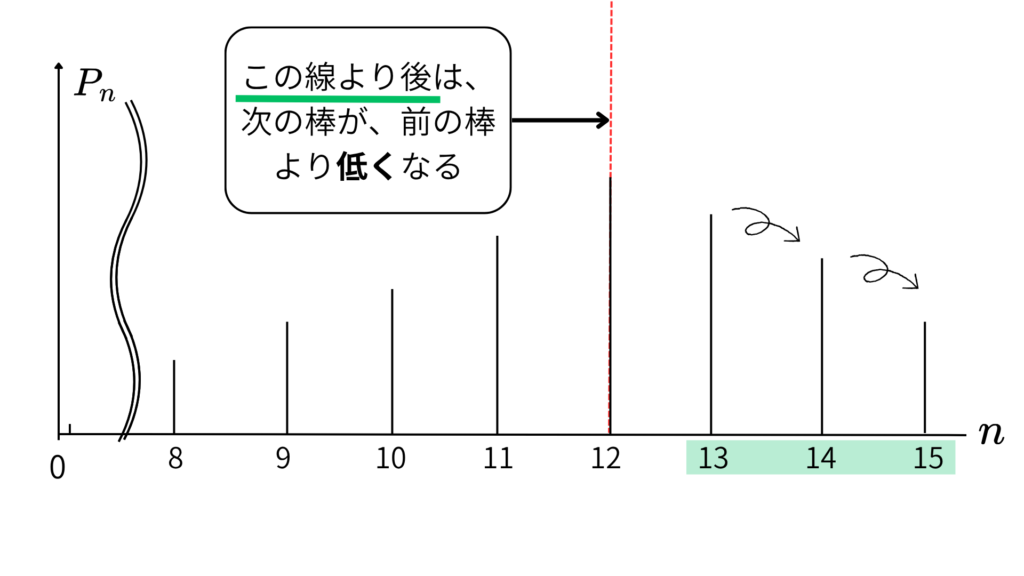
こんな感じになります!!
ただ、今適当に\(\;n=13\;\)の棒を決めたんですけど
実際には、\(\;n=13\;\)の棒の情報は
- \(\;n=12\;\)の棒より高くない
- \(\;n=14\;\)の棒より高い
これだけです、だから
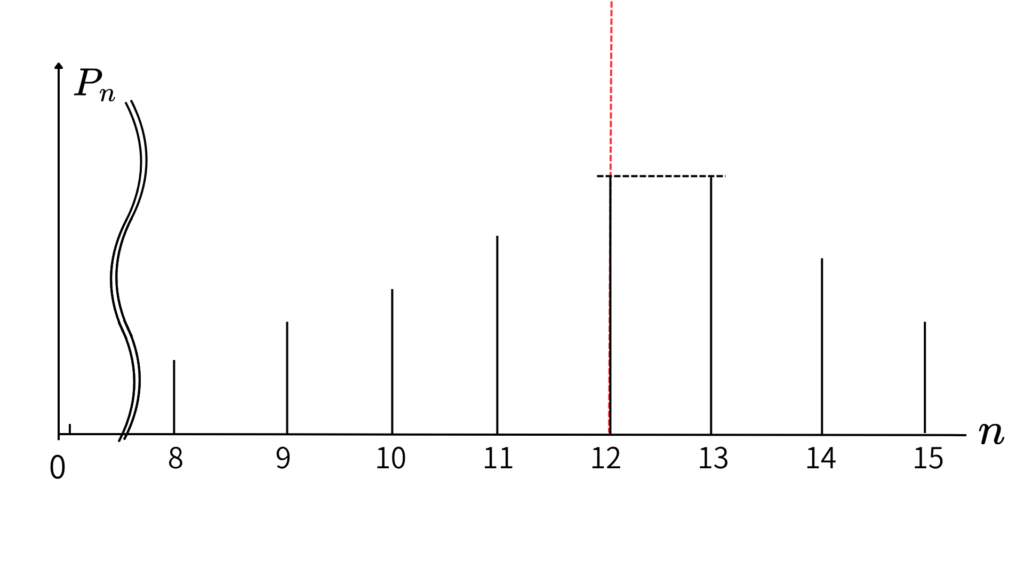
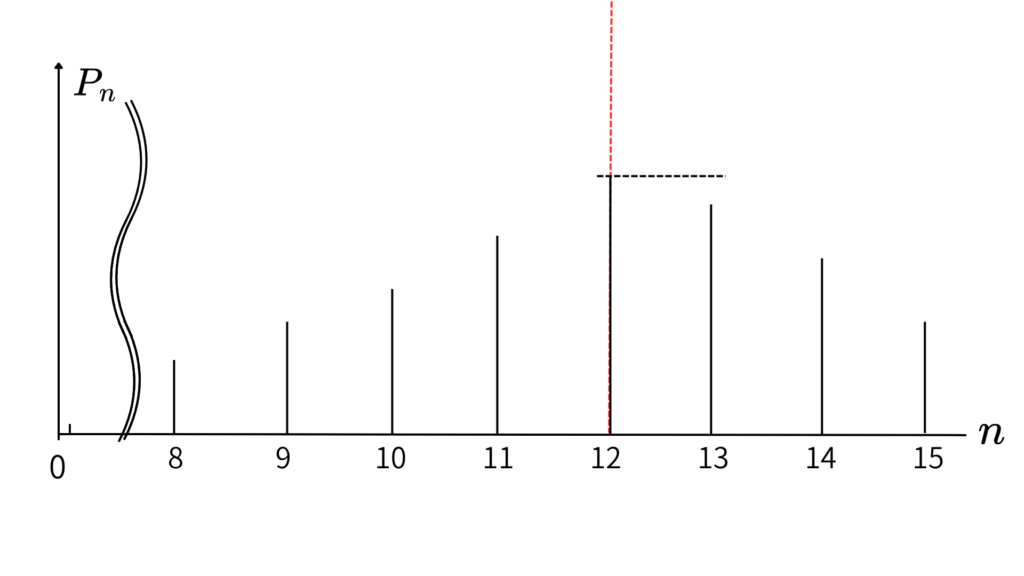
この二つの可能性があります!
こういう時には
\[ \; \frac{P_{n+1}}{P_n}\;= \;\;\frac{n}{(n – 2)}\;(\frac{5}{6})=1\]
を考えるんです!
この時、式を解くと
\(\;n=12\;\)となります!
この時のイメージは
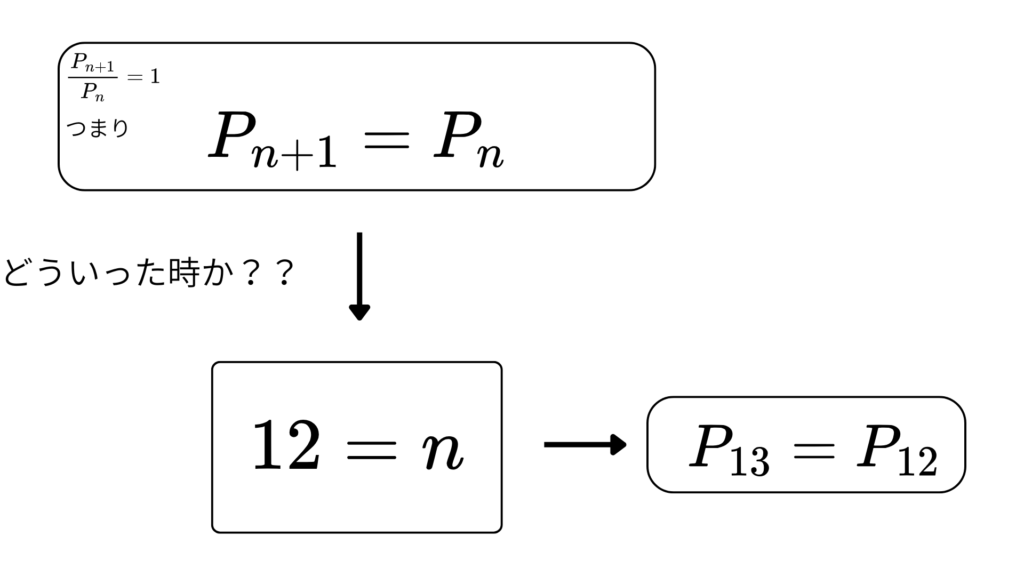
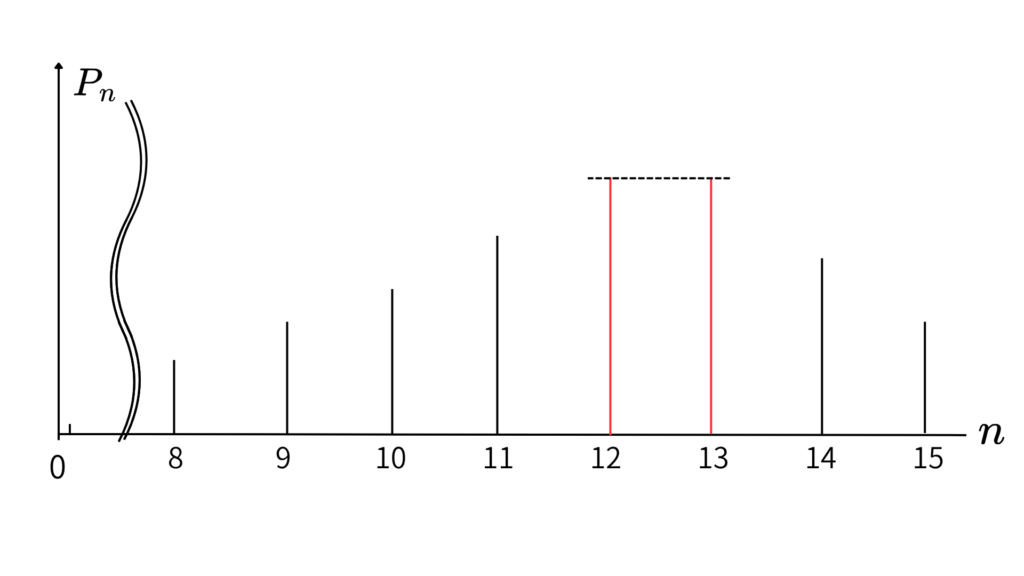
もう図からわかりますね!
最大値は\(\;n=12,13\;\)のとき
3. \(P(N+1)-P(N)\)の正負を調べる
この手順は、確率問題以外のときに使うものです!(あんま使わない…)
確率のときにも出てきた
\[P(N+1)>P(N)\]
つまり
\[P(N+1)-P(N)>0\]
を解きます
ここでこんな疑問を抱く人もいると思います
一言で答えるならこうです
今回の例題でもわかったと思いますが
複雑な式であっても、めちゃくちゃ約分できるんです!!
だから、確率のときは分数を使うんです!
もう1つ、分数であらわすことが確率と相性がいいことがあります
それは、\(P(N)\)が必ず正になるということです
確率が負になるとか意味わかんないですもんね
これのどこが相性がいいのかというと
\[P(N+1)>P(N)\]
この式を\(P(N)\)で割るとき符号が変わらないというところです!
類題でこのタイプの問題を出しておきますね!
2.P(N)のグラフを調べる
たまにこっちのパターンもあるので紹介します
使う目安としては、
こんな感じでOK!
1.\(\;P(N)\;\) を求める
これは完全に1つ目の解法の最初の手順と一緒ですね!
2.f(x)と捉えてグラフを書く
ここで1度、変数を\(\;N\;\)から\(\;x\;\)にします!
このあと、グラフを使った最大最小と同じ解き方をします
置き換えに注意した後、定義域に注意してグラフを書きます
3.グラフから最大、最小となる整数\(\;N\;\)を見つける
再び\(x\;\)から\(\;N\;\)に戻して最大・最小となる整数\(\;N\;\)を見つけます
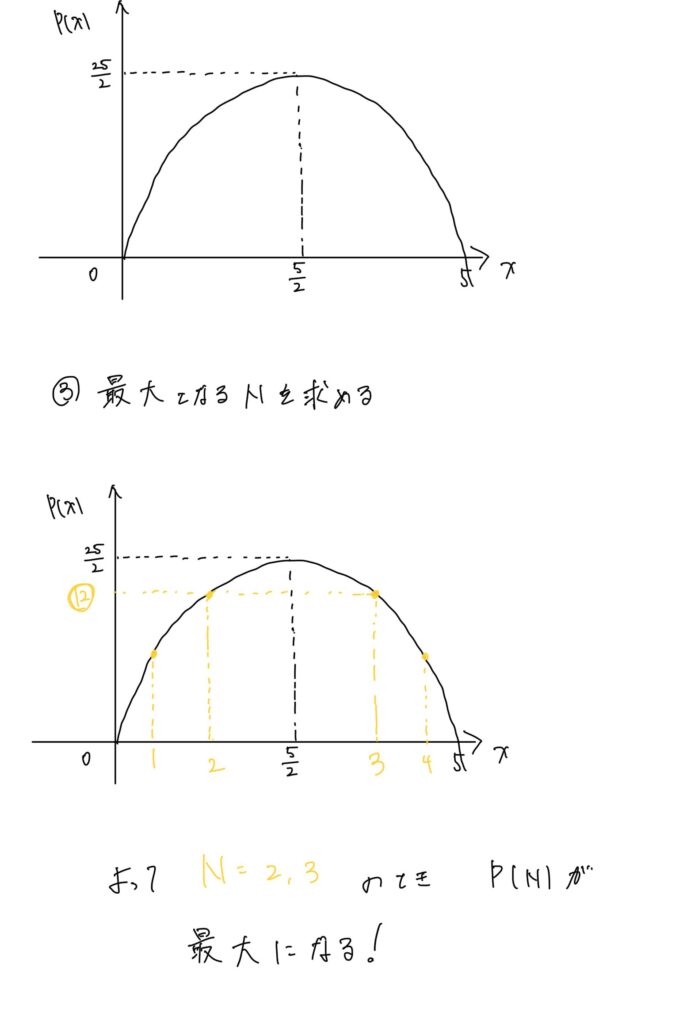
これだけだとイメージがわきにくいと思うので
例を下に書いておきます!

類題
類題を出します!
これらの問題が解けたら、整数関数の最大最小はばっちり!!
自信がなければもう一度Stepを見直そう!
<類題>
(1) 初項21、公差-4の等差数列{\(\;a_n\;\)}の初項から第n項までの和を\(\;S_n\;\)とするとき、\(\;S_n\;\)が最大となる\(\;n\;\)の値を求めよ。
(2) さいころを続けて100回投げるとき、1の目がちょうど\(\;n\;\)回出る確率を\(\;p_n\;\)とする。\(\;p_n\;\)が最大となる\(\;n\;\)の値を求めよ。
解説はこちらから
まとめ
ここまで読んだあなたは、整数関数の最大最小問題の解法ステップが説明できますか?
1.\(P(N+1),P(N) \;\)の関係を調べる
- \(\;P(N)\;\) を求める
- 確率問題なら\(\; \frac{P(N+1)}{P(N)}\;\)と1との大小を調べる
- それ以外なら\(P(N+1)-P(N)\)の正負を調べる
2.\(\;P(N)\; \)のグラフを調べる
- \(\;P(N)\;\) を求める
- 関数\(\;f(x)\;\)と捉えて、グラフを書く
- グラフから最大、最小となる整数\(\;N\;\)を見つける
こうでしたね!
次整数関数の最大最小問題を見たときは一瞬で解いちゃってください!!
まとめ記事の紹介
最大最小のまとめ
1変数多項式の最大最小まとめ


コメント