こんにちは!現役京大生のむぎといいます!
今回は、置き換えの最大・最小の問題を攻略していきます!!
置き換えの問題は、
このような理由から、とても重要なテーマです!
この記事で得られる学び
この記事を読み切るころには次のような学びが得られているでしょう!
- 置き換え問題の基本的な解き方
- 注意点とその対策
- 見落とさない方法
最大最小問題のどこを学ぶの?
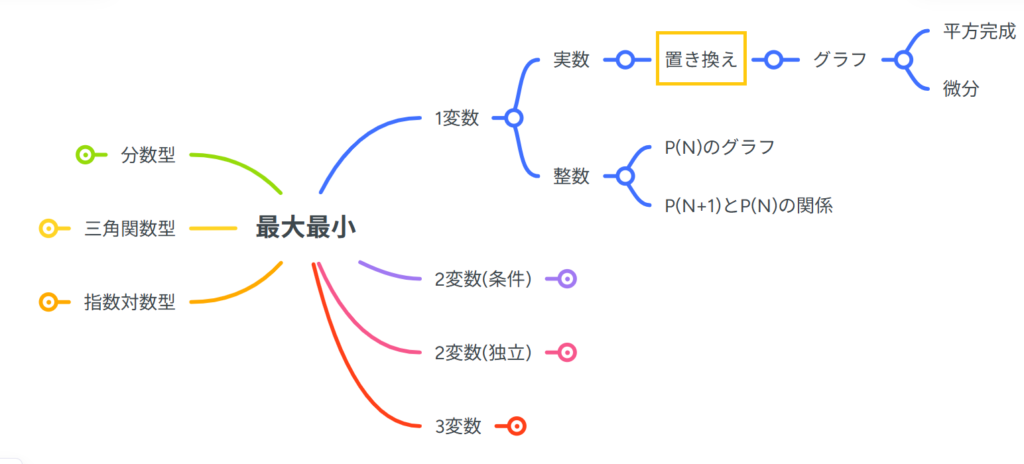
置き換えの問題の全体での位置です!
全体像を知りたい人はこちらのリンクからどうぞ!
例題
今回の例題です
\(x^4-4x^2+6\)の最小値を求めよ
重要度と難易度
| 重要度 | ★★★★☆(4) |
| 難易度 | ★★☆☆☆(2) |
根底にある解き方が様々な分野で応用されるので重要度は高いです!
ミスはしやすいですが、そこさえ気を付ければそこまで難しいわけではありません
解法ステップ
置き換え問題の解法ステップを解説します!
- 置き換えで楽になるかの判断
↓ - 置き替える + 範囲を注意する
↓ - 簡単になった式の最大最小を求める

1つ1つ解説していくね
1.置き換えで楽になる?
\(x^4-4x^2+6\)の最小値を求めよ (例題再掲)
例題を解くとき、そのまま微分して増減表としては大変です
(まだ、微分を習っていない方もいるかもしれません)
しかし例題は置き換えを行うことで数Ⅰの範囲で楽に解くことができます!
つまり、\(x^2=t\)とすると
\(t^2-4t+6\)の最小値を求めよ
というより簡単な問題にすることができます!!
このように置き換えで楽になるかを判断をすることが、第1ステップです!
ただ、ここを忘れてしまうことが多いのです…
しかし、みなさんなら大丈夫です!!
私のフローチャート通りに解くと必然的に置き換えをするかの判断をします
フローチャートのとてもいいところですね!!
置き換えで楽になるかを判断をする
2.置き替える + 範囲を注意する
ここが、置き換え問題を解く時の、1番の注意点です!!
例題でやってみます
- 置き換えをする
\(x^2 = t\) - 範囲を注意する
\(t\) つまり \(x^2\)の範囲は
\(x^2 \geq 0\) より \(t \geq 0\) という隠れた条件が付きます!
この、隠れた条件を見逃すことがとても多いです!!
常に気を付けておきましょう!!
具体的な誤答例を以下に示しておきます
<誤答例>
【問題】\(x^4+4x^2+5\)の最小値を求めよ
【解答】
あー、\(x^2=t\)と置くことで、2次関数になるな
つまり、\(t^2+4t+5\)の最小値を求めればいいんだな
\(t^2+4t+5\)
=\((t+2)^2+1\)
だから、\(t=-2\)のとき、最小値1だな!!
これは範囲を注意し忘れたことによるミスです
ちなみに解答例は次のようになります
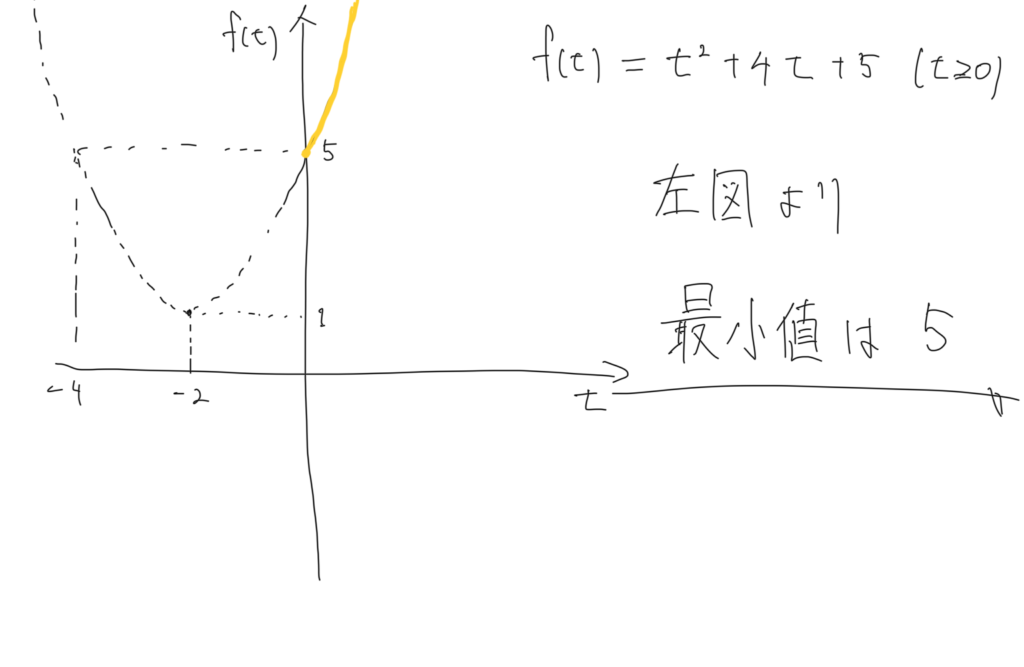
置き換えたら範囲に注意
3.最大最小を求める
ここまで来たら、あとはグラフで
最大値最小値を求めます
これは、↓の記事で勉強をしてください!!
類題
類題を出します!
これらの問題が解けたら、1変数多項式の置き換えの問題はばっちり!!
自信がなければもう一度Stepを見直そう!
<類題>
次の関数の最大、最小を求めよ
(1) \(y = -4x^4+16x^2\)
(2) \(y = (x^2-4x)^2+2(x^2-4x) \)
\(\qquad(-1 \leq x \leq 5) \)
まとめ
ここまで読んだあなたは、置き換えの最大最小問題の解法ステップが説明できますか?
- 置き換えで楽になるかの判断
↓ - 置き替える + 範囲を注意する
↓ - 簡単になった式の最大最小を求める
こうでしたね!
次置き換えの問題を見たときは一瞬で解いちゃってください!!
まとめ記事の紹介
最大最小のまとめ
1変数多項式の最大最小まとめ

コメント