こんにちは!現役京大生のむぎといいます!
今回は、グラフを使う最大・最小の問題を攻略していきます!!
実際、1変数多項式の最大最小は、ほぼすべてがこの解法となります
つまり、ここができなければ、ほぼすべての問題が解けず
できるならば、ほぼすべての問題が解けます!
このような理由から、とても重要なテーマです!
この記事で得られる学び
この記事を読み切るころには次のような学びが得られているでしょう!
- グラフを使う最大最小の基本的な解き方
- これ通りにやればいい!という手順
最大最小問題のどこを学ぶの?
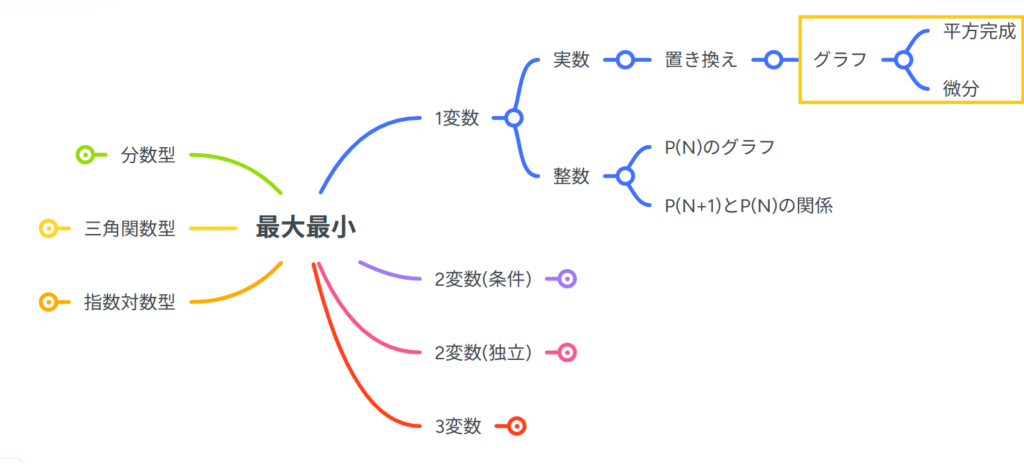
今回の問題の全体での位置です!
全体像を知りたい人はこちらのリンクからどうぞ!
例題
今回の例題です
\(k\;\)は定数とし、\(x\;\)の\(2\)次関数 \(y=x^2-4kx+k^3+k^2-9k+2\) の最小値を\(\;m\;\)とする。
(1)\(\;m\;\)を\(\;k\;\)の式で表せ。
(2)\(k\;\) の値を\( \;-2 \leq k \leq 4\; \)の範囲で変化させたとき、\(m\;\)の最大値を求めよ。
重要度と難易度
| 重要度 | ★★★★★(5) |
| 難易度 | ★★☆☆☆(2) |
最大最小問題の一番の基礎となる部分で、様々な分野で応用されるので重要度は高いです!
応用問題(定義域に\(\;a\;\)を含み場合分けが必要など)は難易度が高くなります
基礎をしっかり理解しないと、応用に歯が立ちません
まず、今回の内容をしっかり確認しましょう!!!
解法ステップ
グラフを使う最小問題の解法ステップを解説します!
- 定義域に注意してグラフを書く
↓ - 端点、頂点に注目してその中で最大最小を求める

1つ1つ解説していくね
1.定義域に注意してグラフを書く
\(k\;\)は定数とし、\(x\;\)の\(2\)次関数 \(y=x^2-4kx+k^3+k^2-9k+2\) の最小値を\(\;m\;\)とする。
(1)\(\;m\;\)を\(\;k\;\)の式で表せ。
(2)\(k\;\) の値を\( \;-2 \leq k \leq 4\; \)の範囲で変化させたとき、\(m\;\)の最大値を求めよ。 (例題再掲)
まず、最初の手順としてグラフを書きます
この時、
- 2次関数 → 平方完成
- 3次以上の関数 → 微分
↑は1つの大事な目安となります
グラフを書くとなったら0.01秒くらいで平方完成、または微分をしましょう!!
例題のここまでの思考回路を、再現します
\(m\;\)の最小値を求めるのか…つまり (1) は最大最小問題だ!!
大まかな分類ではどうなるの?
\(k\;\)は定数だから\(\;y\;\)の式は\(\;x\;\)の1変数多項式となる!
まず、実数か整数か?…
実数!!
置き換えはできなさそう…
よし、グラフを書こう!!
えーーっと、\(\;x\;\)の2次式だかrr
平方完成!!!!!!!(0.01秒)
こんな感じですね(笑)
1つ1つフローチャートをたどるのは面倒くさいと思うかもしれませんが、
慣れれば速くできるし、何より試験本番で安定して得点できます!!
続きは定義域に注意をしてグラフを書いていきます!
\(y=x^2-4kx+k^3+k^2-9k+2\;\)を平方完成すると
\(y=(x-2k)^2+k^3-3k^2-9k+2\;\)
定義域の制限は特になさそうだから
そのままグラフを書くと…
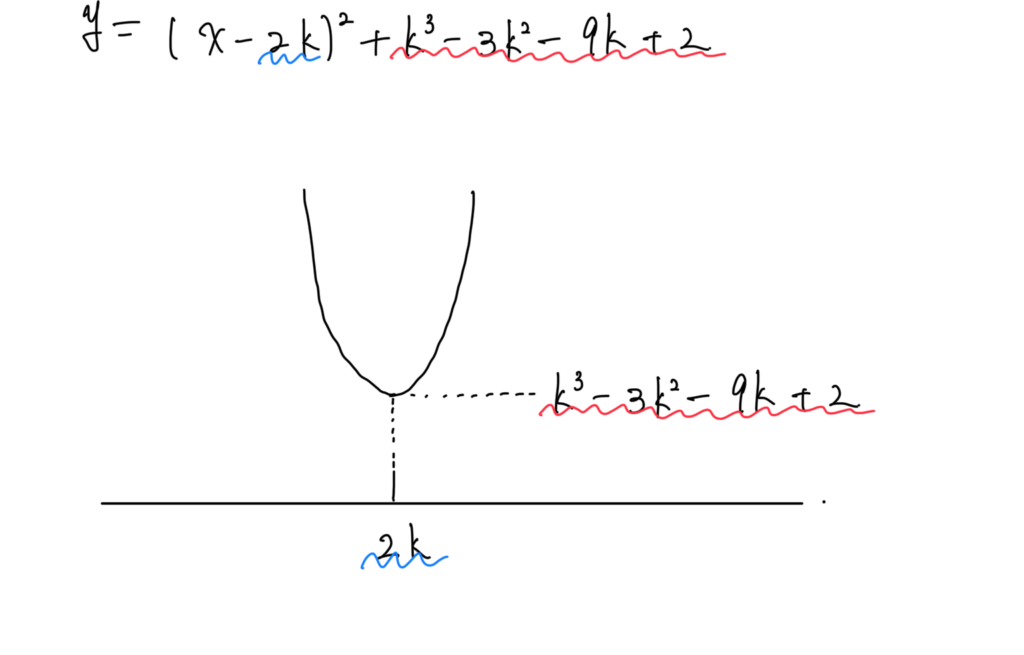
1.グラフを書く 完了!!
2.端点、頂点に注目してその中で最大最小を求める
先ほど、書いたグラフから、最大値、最小値候補に注目します
それが、端点と頂点です
実際に例題で見てみましょう!
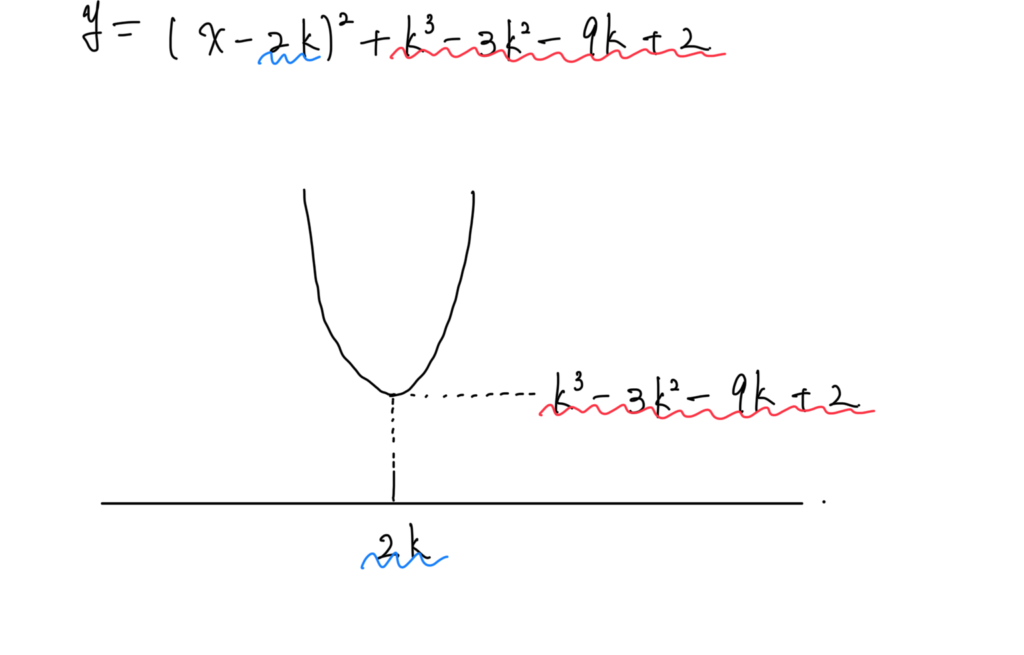

よろしいでしょうか??
(3)をやってみよう!!
これまでの復習として、(3)をやってみましょう!!
3次関数ということは…?
解答



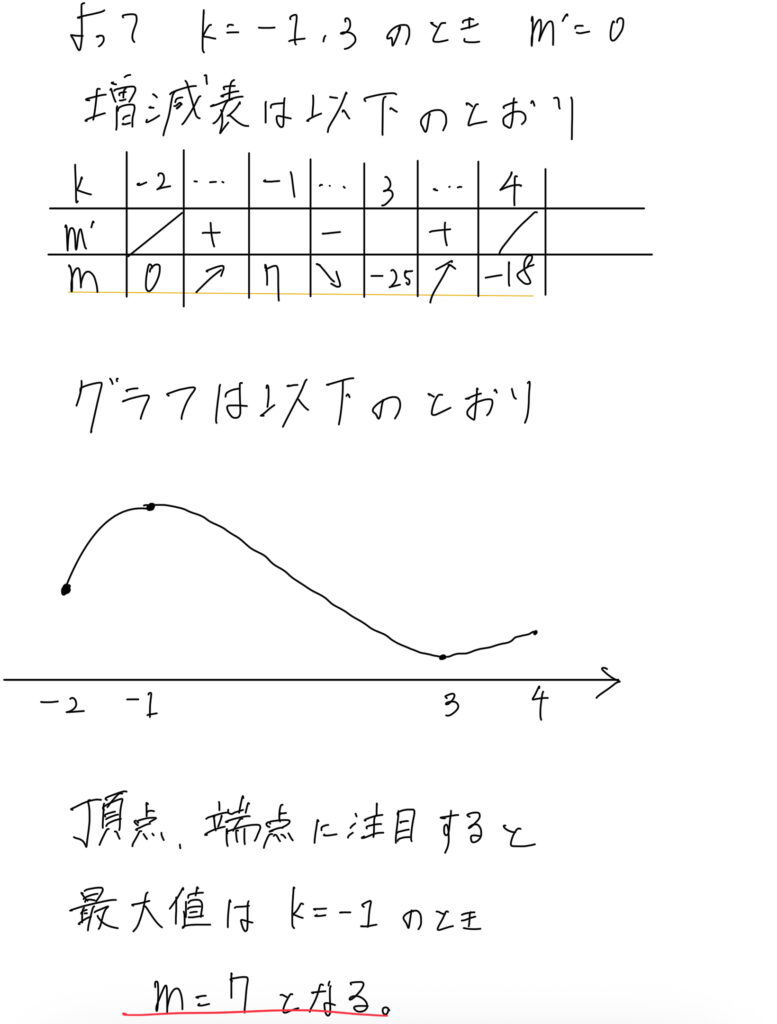
類題
類題を出します!
これらの問題が解けたら、1変数多項式のグラフを使った最大最小の問題はばっちり!!
自信がなければもう一度Stepを見直そう!
<類題>
次の\(\;y\;\)の最大値\(\;M\;\),最小値\(\;m\;\)をそれぞれ求めよ。
(1) \(\quad y = x^2|x-1| \qquad (-2 \leq x \leq 2) \)
(2) \(\quad y = x^2-4x+5\qquad (a \leq x \leq a+1) \) \(\qquad (a\;\)は定数)
解説はこちらから
まとめ
ここまで読んだあなたは、グラフを使う最大最小問題の解法ステップが説明できますか?
- 定義域に注意してグラフを書く
↓ - 端点、頂点に注目してその中で最大最小を求める
こうでしたね!
次グラフを使う最大最小問題を見たときは一瞬で解いちゃってください!!
まとめ記事の紹介
最大最小のまとめ
1変数多項式の最大最小まとめ

コメント