こんにちは!現役京大生のむぎといいます!
皆さん最大最小問題に次のような悩みを抱えてないですか?
でも大丈夫です!!最大・最小問題は「型」で解けてしまいます!!
この記事で得られるもの
- 2変数関数の最大最小問題の、解法フローチャート
- 自信を持ち迷わず解き進める力
- 安定的な得点力
- ほぼすべての解法パターン
全体像を見てみよう!
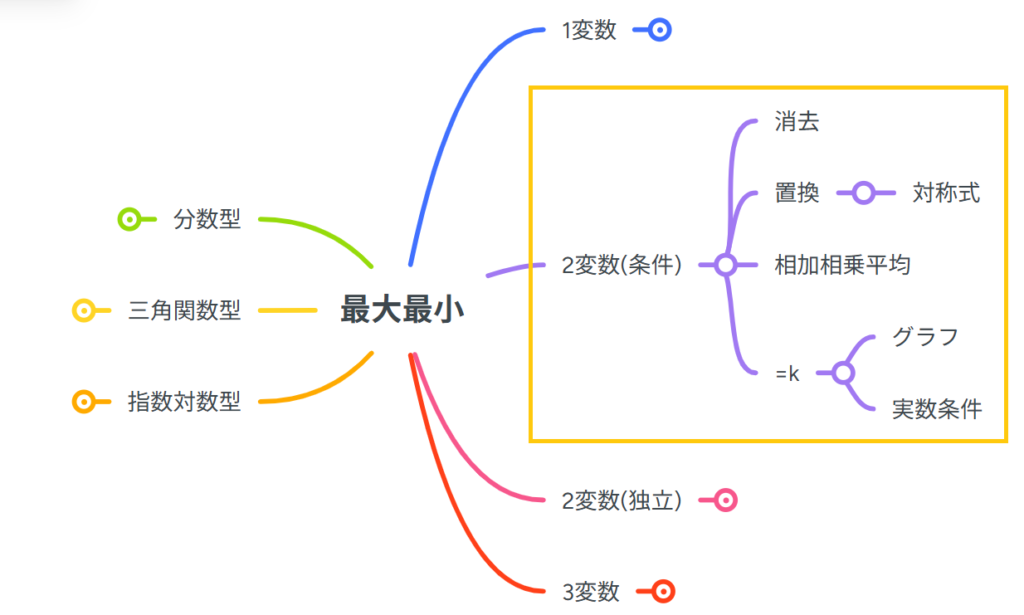
今回は、画像の黄色い線で囲まれたところを勉強するよ!!
最大最小のまとめ記事をまだご覧になっていない方は、ぜひご覧ください!!
【条件式】2変数関数の最大最小って何??
条件式付きの2変数関数の最大最小とは
たとえば、
\(x+y=6\;\)
\(\;x+2y\geq0\;\)
のように条件式が付いた状態で
\(x^2-4xy+5y^2\;\)の最小値を求めよ
のように2変数の式の最大最小を求める問題です!!

早速、フローチャートを見ていくよ!!
【条件式】2変数関数の最大最小の解法フローチャート
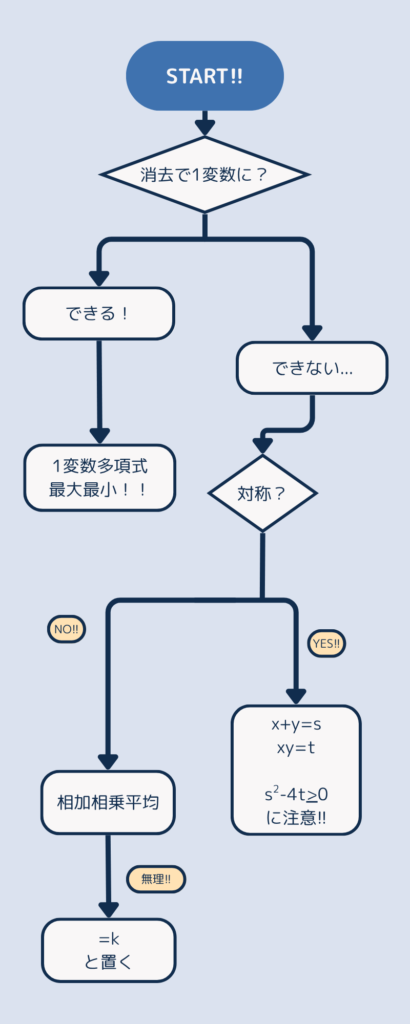

このフローチャートを保存して、いつでも見返せるようにしよう!
フローチャートの各ステップを深掘り!
実際に、フローチャートでの解法を解説します!
ただし、ここではまとめるととても長くなってしまうので、大まかな説明をします。
解法の詳しい説明については、貼られているリンクからお願いします!!
1.消去できる?
まず、消去できるか、で分類します
今回は条件式がある2変数関数なので、
1文字を消去できる可能性があります!!
例えば、
\(x+y=4\;\)とする
\(x^2-4xy+5y^2\;\)の最小値を求めよ
このような問題があったとします
まず、文字消去ができるかを確認します!
すると、\(x+y=4\;\)から\(\;y=4-x\;\)として代入すれば
\(y\;\)を消去できることがわかります!
\(x+y=4\;\)とする
\(x^2-4xy+5y^2\;\)の最小値を求めよ
↓ \(\;y=4-x\;\)
\(x^2-4x(4-x)+5(4-x)^2\)
つまり
\(10x^2-56x+80\;\)の最小値を求めよ
このようにして、1変数関数の最大最小に持ち込むことができます!
1変数関数の最大最小は結構簡単な解法しかないので、勝ちですね(笑)
(こちらの記事で解説しています!見ていない方はぜひ見てください!)
簡単そうに見える文字消去でも、実は減点ポイントがあります!
その対策を↓の記事で解説しているので、ぜひ見てみてください!!
2.対称であるか?
とはいえ、そんな簡単な問題は多くはありません!
消去できないことも多くあります!
ここに、多変数の最大最小の難しさが詰まっています
解法が結構多く、難しいんですね
ここを、フローチャートで解くことで、突破していきます!
まず、見なきゃいけないのは、対称であるか?です
例えばこんな問題
\(x^2+xy+y^2=3\;\)とする
\(x^2+y^2+2(x+y)\;\)の最大値、最小値を求めよ。
この問題では、文字消去がうまくいかない場合です
そこで、文字の対称性がないかの確認です!
対称性があるとは
文字を入れ替えても式が変わらない状態のことです
今回の問題では\(\;x\;\)と\(\;y\;\)を入れ替えても式が変わらないので、
対称性があるといえます
このような問題のときは
\(x+y=s\;\)
\(xy=t\;\)とする
ことで、うまくいくことが多いです
ただこの問題は、間違えやすいポイント、理解が難しい、という問題があります
そこで、この問題に困っている方のために、できるだけ分かりやすくまとめた記事を貼っておくのでぜひマスターしてください!!
3.相加相乗平均
ここまでのパターンが当てはまらなかったときは、相加相乗平均を試してみましょう!
【相加相乗平均】
\(\;a>0,b>0\;\)のとき
\[a+b \geq 2\sqrt{ab}\;\]
等号成立は\(\;a=b\;\)
この不等式を使います
簡単な例でいえば
\(\;a>0,b>0\;\)とする。
\(\;ab=8\;\)のとき、\(\;a+2b\;\)の最小値を求めよ。
この問題では、1文字消去もできますが、相加相乗平均を使うことで楽に解けます!
\(\;a>0,b>0\;\)であるので
相加相乗平均より
\(\;a+2b \geq \sqrt{a(2b)}=\sqrt{2(ab)}=\sqrt{16}=4\;\)
ただし、等号成立条件は\(\;a=2b\;\)
つまり、\(\;ab=8\;\)に注意すると
\(\;(a,b)=(4,2)\;\)
こんな感じですね!
相加相乗平均を使うときは、等号成立条件に触れないと必ず減点されます
相加相乗平均について、練習問題も載せた記事を貼っておくので、見てみてください!
4.=kとする
最終手段です
=kとする解法です。
=kとする中でも2つの解法があります
1.=kとしてグラフから共有点を持つようにkを動かす
2.=kとして実数条件を考える
実数条件…?
となる方も多いと思います
少し説明が長引きそうなので、↓の記事からお願いします!!
まとめ!
条件式ありの2変数関数の最大最小はどうでしたでしょうか??
今回紹介した解法をマスターすれば、条件式ありの2変数関数の最大最小で点が取れるようになります!!
この分野の最大最小については、もう怖いものはありません!
完全な得点源にしましょう!

コメント