こんにちは!現役京大生のむぎといいます!
今回は、文字消去の最大・最小の問題を攻略していきます!!
文字消去の問題は、
このような理由から、とても重要なテーマです!
この記事で得られる学び
この記事を読み切るころには次のような学びが得られているでしょう!
- 減点ポイント
- その対処法
最大最小問題のどこを学ぶの?
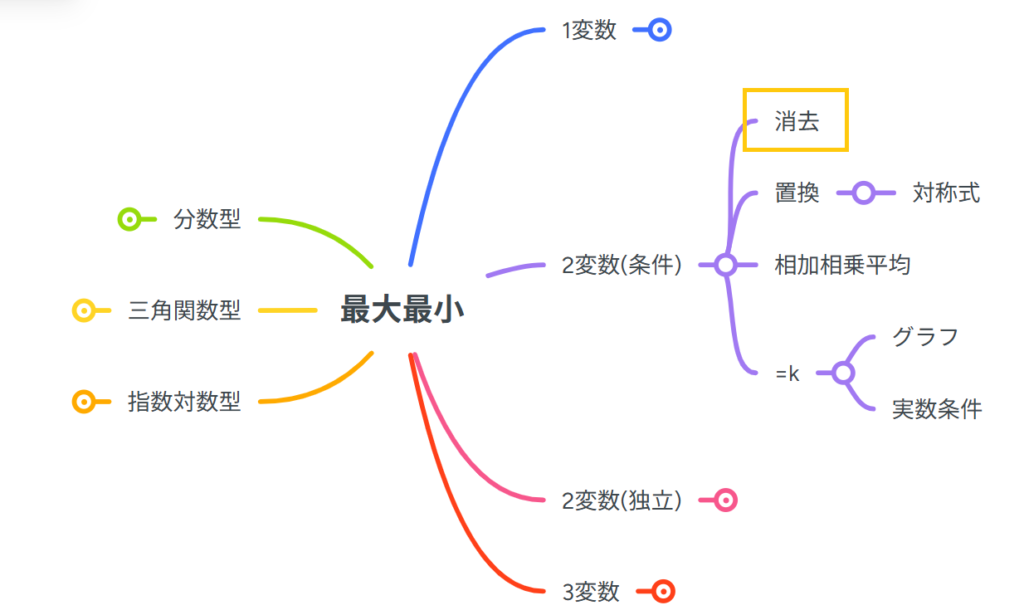
文字消去の問題の全体での位置です!
全体像を知りたい人はこちらのリンクからどうぞ!
例題
今回の例題です
\(\;x,y\;\)を実数とする。\(x^2+y^2=4\;\)のとき
\(2x+y^2\;\)の最大値、最小値を求めよ。
重要度と難易度
| 重要度 | ★★★★☆(4) |
| 難易度 | ★★☆☆☆(2) |
文字消去はしょっちゅうするのでので重要度は高いです!
あんまり難しくないですが、減点されないように、対策を学びましょう!!
解法ステップ
文字消去の解法ステップを解説します!
- 文字消去をする
↓ - 範囲に注意する
↓ - 1変数多項式の最大最小を求める

1つ1つ解説していくね
1.文字消去をする
\(\;x,y\;\)を実数とする。\(x^2+y^2=4\;\)のとき
\(2x+y^2\;\)の最大値、最小値を求めよ。(例題再掲)
普通に文字消去すれば大丈夫です!
\(x^2+y^2=4\;\)より
\(y^2=4-x^2\;\)
これを使って\(\;y^2\;\)を消去すると
\(2x+y^2=2x+(4-x^2)\;\)
\(2x+4-x^2\;\)の最大最小を求める
2.範囲に注意する
ここが、文字消去の問題を解く時の、1番の注意点です!!
さっきのままだと\(\;x\;\)の定義域は実数全体になりますが
たとえば、\(\;x=3\;\)だとしましょう
\[x^2+y^2=4\;\]
に\(\;x=3\;\)を代入すると
\[y^2=-5\;\]
となり、\(\;y\;\)が実数じゃなくなります!
このような事態を防ぐためにこれを覚えておいてください
“置き換えたら範囲に注意”と一緒に覚えておきましょう!!
今回の例題でやると
\(y^2=4-x^2\;\)
これを使って\(\;y^2\;\)を消去すると
\(2x+y^2=2x+4-x^2\;\)
\(2x+4-x^2\;\)の最大最小を求める
ただし、\(\;y^2\;\)を消去するので
\(y^2\;\)の範囲に注意する!
\(\;y^2 \geq 0\;\)であるので、\(y^2=4-x^2 \geq 0\;\)
\[-2 \leq x \leq 2 \;\]
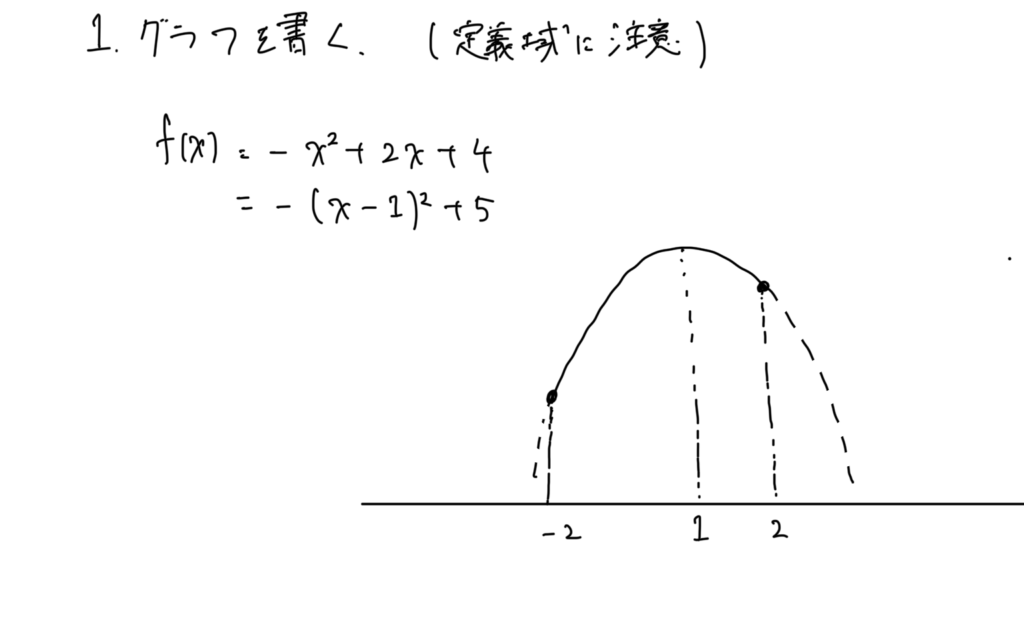
3. 1変数多項式の最大最小を求める
あとは、1変数多項式の最大最小を求めます!!
これは、以前ほかの記事で解説していたので、それを見てみてください!


類題
類題を出します!ちょっとむずめ!
これらの問題が解けたら、文字消去の最大最小の問題はばっちり!!
自信がなければもう一度Stepを見直そう!
<類題>
\(\;x,y\;\)は実数とする。
\(\;2x+y=8 ,x \geq 0,y \geq 0\;\)のとき
(1)\(\;xy\;\)の最大最小を求めよ
(2)\(\;x^2y^2+4x^2+y^2\;\)の最小値を求めよ
ヒント
(2)は(1)を利用
解説はこちらから
まとめ
ここまで読んだあなたは、文字消去の最大最小問題の解法ステップが説明できますか?
- 文字消去をする
↓ - 範囲に注意する
↓ - 1変数多項式の最大最小を求める
こうでしたね!
次文字消去の最大最小の問題を見たときは一瞬で解いちゃってください!!
まとめ記事の紹介
最大最小のまとめ
【条件式】2変数関数の最大最小まとめ

コメント