こんにちは!現役京大生のむぎといいます!
今回は整数関数の最大・最小の類題の解説をします!
主な例として
- 確率の最大最小
- 数列の最大最小
があります!!
整数関数の最大・最小はこちらの記事で説明しています

類題まで解くと、ほんっとに力になる!!
類題を通して、知識を固めていきましょう!!
類題
<類題>
(1) 初項21、公差-4の等差数列{\(\;a_n\;\)}の初項から第n項までの和を\(\;S_n\;\)とするとき、\(\;S_n\;\)が最大となる\(\;n\;\)の値を求めよ。
(2) さいころを続けて100回投げるとき、1の目がちょうど\(\;n\;\)回出る確率を\(\;p_n\;\)とする。\(\;p_n\;\)が最大となる\(\;n\;\)の値を求めよ。
解説
(1)数列の最大最小
まずはフローチャートをたどります!
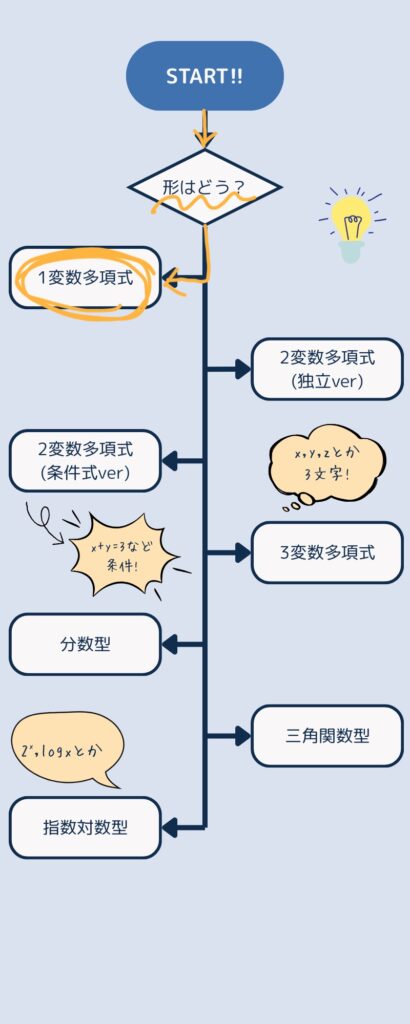
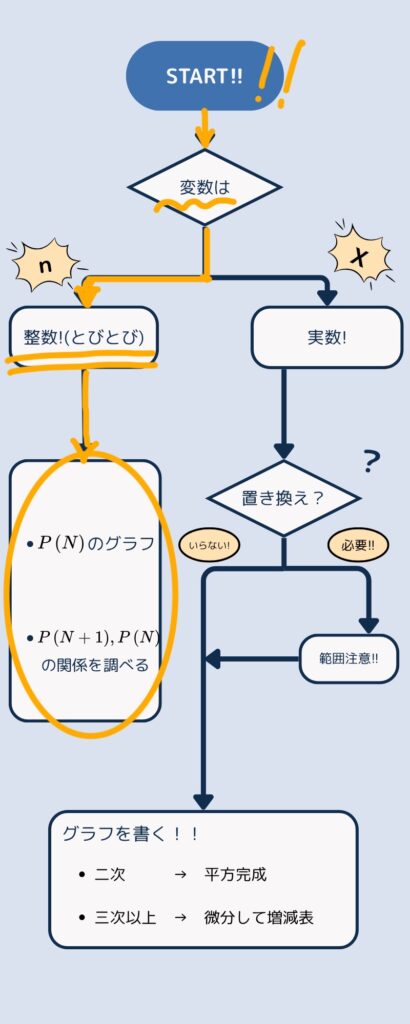
さあ、ここの解法はどうだったでしょうか??
解法1.\(P(N+1),P(N) \;\)の関係を調べる
- \(\;P(N)\;\) を求める
- 確率問題なら\(\; \frac{P(N+1)}{P(N)}\;\)と1との大小を調べる
- それ以外なら\(P(N+1)-P(N)\)の正負を調べる
解法2.\(\;P(N)\; \)のグラフを調べる
- \(\;P(N)\;\) を求める
- 関数\(\;f(x)\;\)と捉えて、グラフを書く
- グラフから最大、最小となる整数\(\;N\;\)を見つける
こうですね!!
まず、解法1でやってみます!
1.\(\;P(N)\;\) を求める
今回、\(\;P(N)\;\)にあたるものは、\(\;S_n\;\)です。
\(\;S_n\;\)は、初項21、公差-4の等差数列{\(\;a_n\;\)}の初項から第n項までの和なので、まず\(\;a_n\;\)を求めると
\(\;a_n=-4(n-1)+21\;\)
\(\;S_n=a_1+a_2+a_3+\ldots+a_n\;\)なので
\(\;S_n=\sum_{k=1}^{n} a_k\;\)
\(\;S_n=\sum_{k=1}^{n} -4k+25\;\)
\(\;S_n=-4*(\frac{1}{2}n(n+1)+25n\;\)
\(\;S_n=-2n^2+23n\;\) となります!
2.確率問題なら\(\; \frac{P(N+1)}{P(N)}\;\)と1との大小を調べる
確率問題じゃないのでスキップ!
3.それ以外なら(P(N+1)-P(N))の正負を調べる
\(\;S_{n+1}-S_{n}\;\)を求めます!
\(\;=-2(n+1)^2+23(n+1)+2n^2-23n\;\)
\(\;=-4n+21\;\)ですね!!
(もちろん、「\(\;S_{n+1}-S_{n}\;\)って\(\;a_{n+1}\;\)のことじゃん」とできるならそれが一番早いです!けど、フローチャートでも、遅くても確実に進められます!)
これで、\(\;S_{n+1}-S_{n}\;\)が求まりました!!
今からは正負を調べていきましょう!!
(i)\(\;S_{n+1}-S_{n}>0\;\)のとき
\(\;-4n+21>0\;\)
\(\;21>4n\;\)
\(\;\frac{21}{4}>n\;\)
図で考えるとどうなるでしょうか?
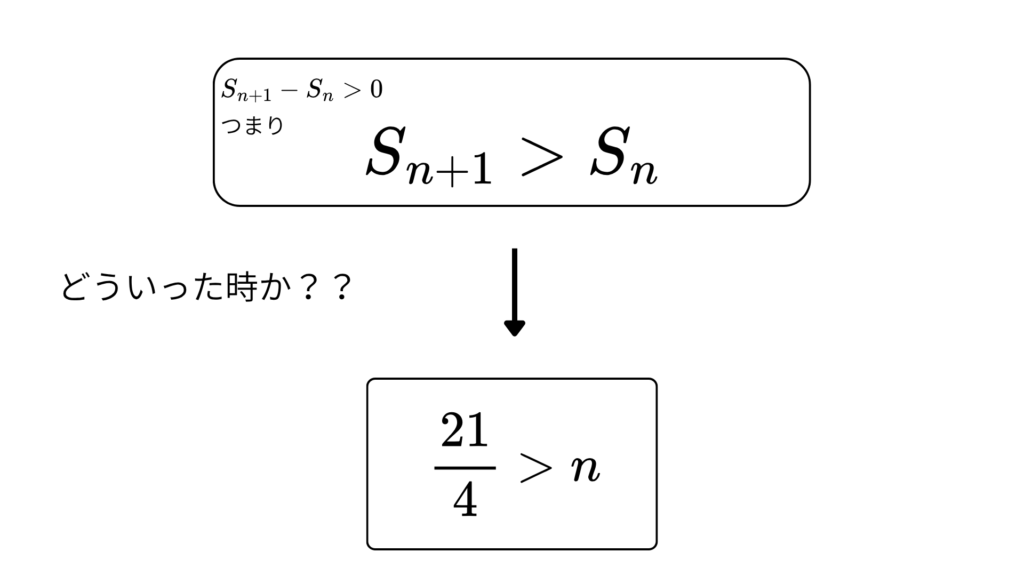
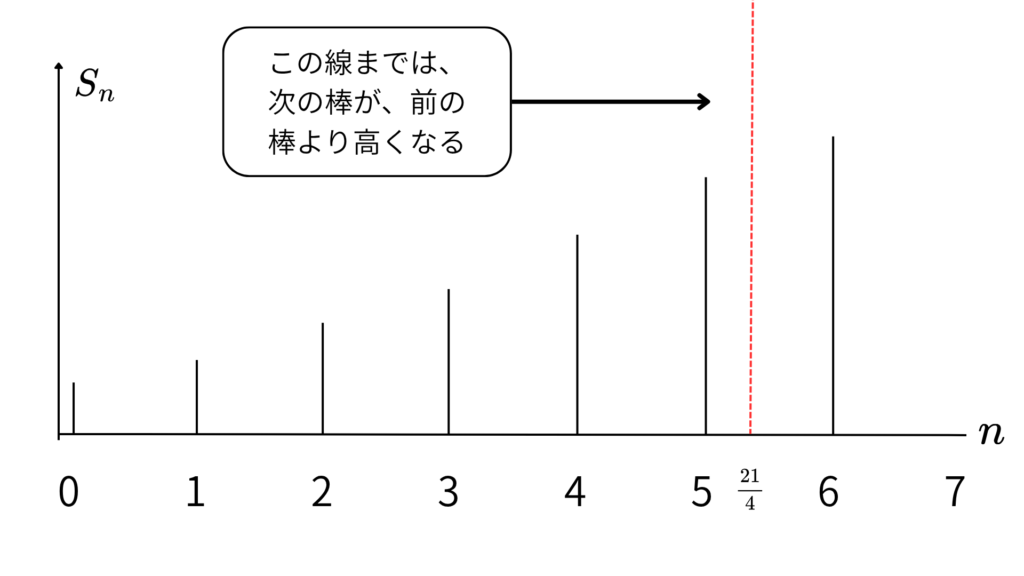
このような感じですね!!
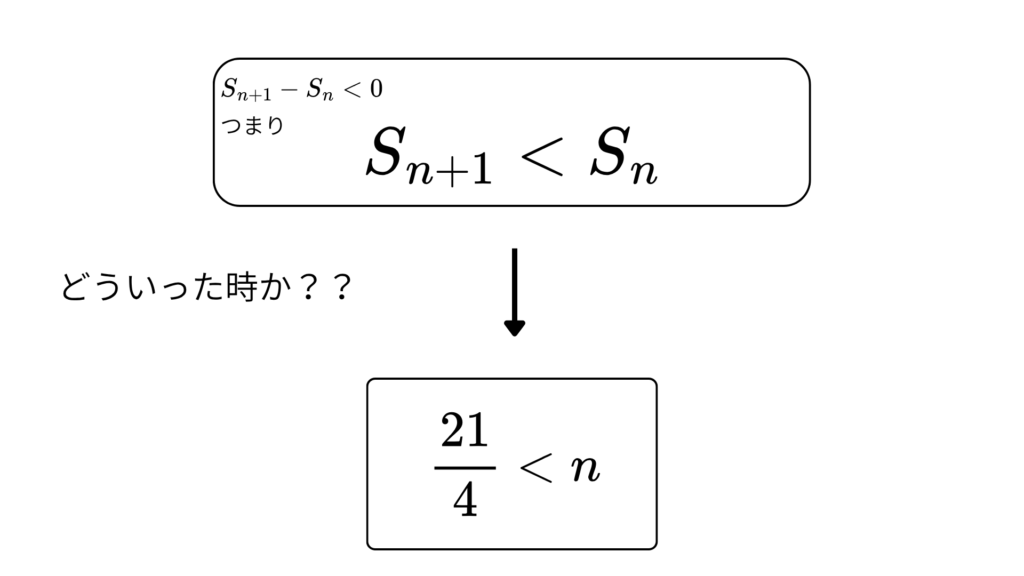
(ii)\(\;S_{n+1}-S_{n}<0\;\)のとき、も求めてみましょう!
(i)と不等号の向きが変わっただけなので
\(\;\frac{21}{4}<n\;\)
こうなります!!
イメージ図はこんな感じ!
さっきとは、不等号の向きが違うのに注意!!
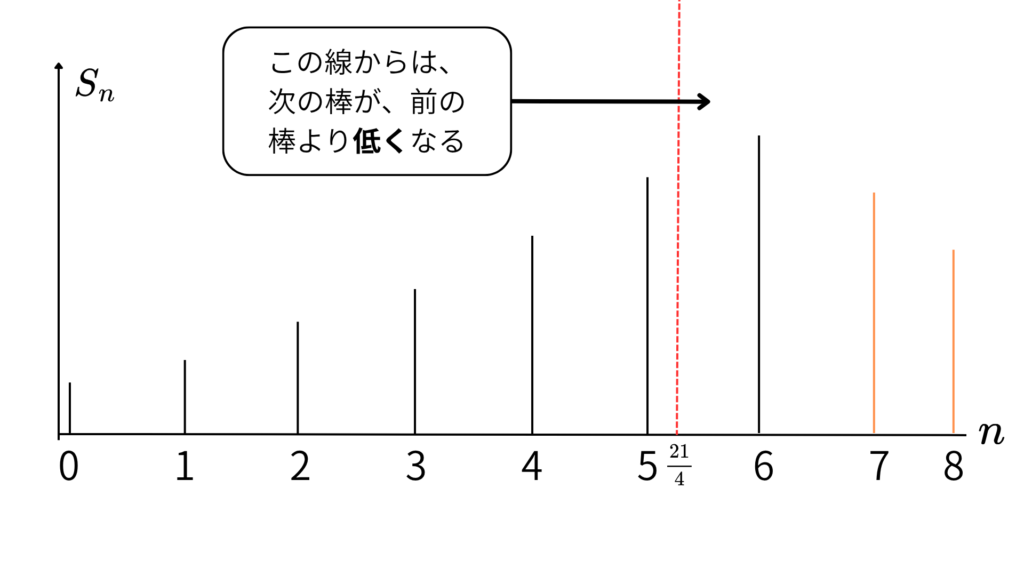
あとは、図からわかる通り!!
\(\;S_n\;\)が最大となる\(\;n\;\)の値は、\(\;n=6\;\)
じゃあ次に解法2でもやってみましょうか!
1.\(\;P(N)\;\) を求める
解法1でやったことと同じです!!
\(\;S_n=-2n^2+23n\;\) となります!
2.関数\(\;f(x)\;\)と捉えて、グラフを書く
いったん、\(\;S_n=-2n^2+23n\;\)を
\(\;f(x)=-2x^2+23x\;\)と捉えます!!
そしてグラフを書いていきます!
グラフの書き方
- 2次関数 → 平方完成
- 3次以上の関数 → 微分して増減表
今回は2次関数なので、平方完成します
\(\;f(x)=-2x^2+23x\;\)
\(\:\:\qquad=-2(x^2-\frac{23x}{2})\;\)
\(\:\:\qquad=-2\{(x-\frac{23}{4})^2-\frac{23^2}{4^2}\}\;\)
\(\:\:\qquad=-2(x-\frac{23}{4})^2+\frac{23^2}{8}\;\)
つまりグラフは、
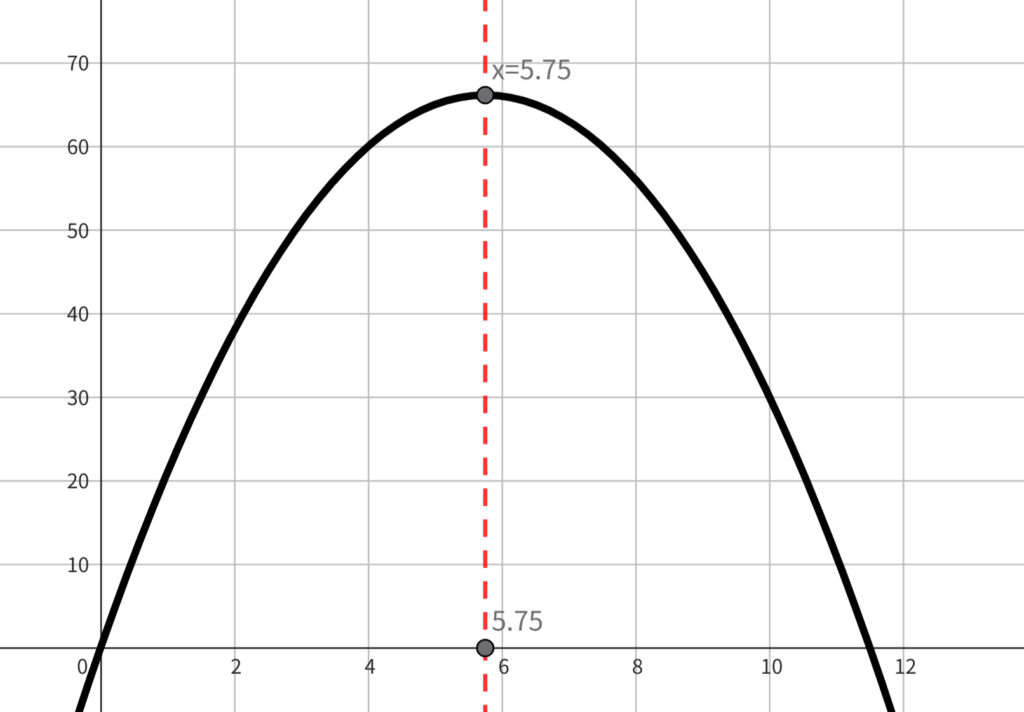
3.グラフから最大、最小となる整数\(\;N\;\)を見つける
グラフから、てっぺんに一番近い\(\;N\;\)を求めます!!
今のままでは、\(\;x=5.75\;\)が最大になるんですが
本来は、\(\;x\;\)ではなく、\(\;n\;\)なので、整数しか取れないんですね
だから、てっぺんに一番近い\(\;N\;\)を求めるんですね!!
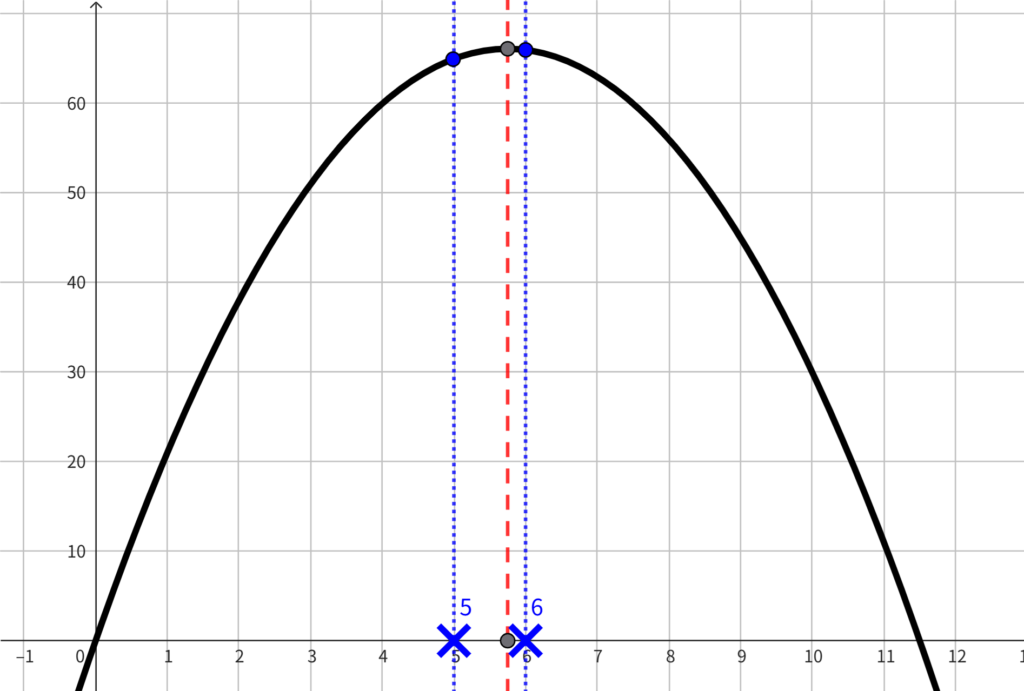
グラフを見ると…
\(\;S_n\;\)が最大となる\(\;n\;\)の値は、\(\;n=6\;\)
(2)確率の最大
まずはフローチャートをたどります!
(1)と同じ流れなので見たい人だけ見てください!
フローチャートの流れ!!


何度もしつこいですが
整数関数の最大最小問題の解法パターンは…
解法1.\(P(N+1),P(N) \;\)の関係を調べる
- \(\;P(N)\;\) を求める
- 確率問題なら\(\; \frac{P(N+1)}{P(N)}\;\)と1との大小を調べる
- それ以外なら\(P(N+1)-P(N)\)の正負を調べる
解法2.\(\;P(N)\; \)のグラフを調べる
- \(\;P(N)\;\) を求める
- 関数\(\;f(x)\;\)と捉えて、グラフを書く
- グラフから最大、最小となる整数\(\;N\;\)を見つける
また、(1)で説明はしませんでしたが、
解法1、解法2の使い分け方は
こんな感じで大丈夫です!!
まず、解法1でやってみます
1.\(\;P(N)\;\) を求める
今回は、さいころをたくさん投げる
反復試行の確率ですね
よって
を使います
今回は投げる回数が100回なので、
\(\;n\;\)→100
“あること”が1の目が出るなので、
\(\;p\;\)→\(\;\frac{1}{6}\;\)
“何回起こるか”\(\;n\;\)回なので
\(\;k\;\)→\(\;n\;\)
よって求める確率、
さいころを続けて100回投げるとき、1の目がちょうど\(\;n\;\)回出る確率は
\[\;P_n={}_{100}C_{n}(\frac{1}{6})^n(\frac{5}{6})^{100-n}\;\]
こうなります!!
2.確率問題なら\(\; \frac{P(N+1)}{P(N)}\;\)と1との大小を調べる
というわけで、\(\; \frac{P(N+1)}{P(N)}\;\)を求めていきます!
この時のポイントを再確認すると
- \(\;{}_{n}C_{k}\;=\frac{n!}{k!(n – k)!}\)を使う
- 分数にして約分!!
でしたね!!
まず、\(\;{}_{n}C_{k}\;=\frac{n!}{k!(n – k)!}\)を使いましょう
\[\;{}_{100}C_{n}\;=\frac{100!}{n!(100 – n)!}\]
こうですね!
これを使って\(\;P_n\;\)を書き直すと
\[\;P_n=\frac{100!}{n!(100 – n)!}(\frac{1}{6})^n(\frac{5}{6})^{100-n}\;\]
あとは…分数にするだけ!!!
\[\;\frac{P_{n+1}}{P_n}=\frac{\frac{100!}{(n+1)!(99 – n)!}(\frac{1}{6})^{(n+1)}(\frac{5}{6})^{99-n}}{\frac{100!}{n!(100 – n)!}(\frac{1}{6})^n(\frac{5}{6})^{100-n}}\;\]
約分していくと
\[\;=\frac{\frac{1}{(n+1)}(\frac{1}{6})}{\frac{1}{(100 – n)}(\frac{5}{6})}\;\]
\[\;=\frac{(100-n)}{5(n+1)}\;\]
できました!!
やってることは単純ですね!
次に1との大小を比べます
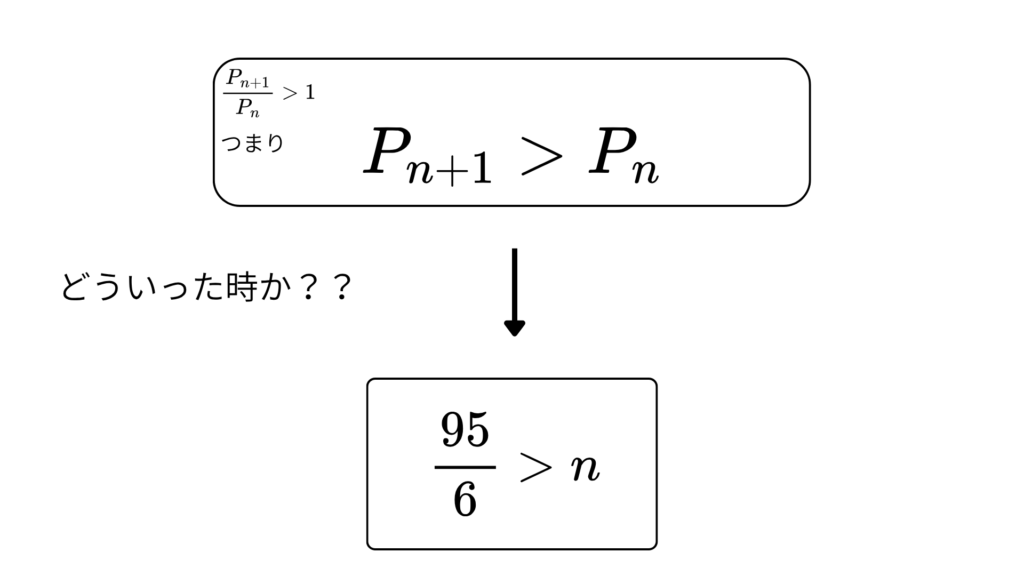
(i)\(\;\frac{(100-n)}{5(n+1)}>1\;\)の時
\(\;(100-n)>5(n+1)\;\)
\(\;95>6n\;\)
\(\;\frac{95}{6}>n\;\)
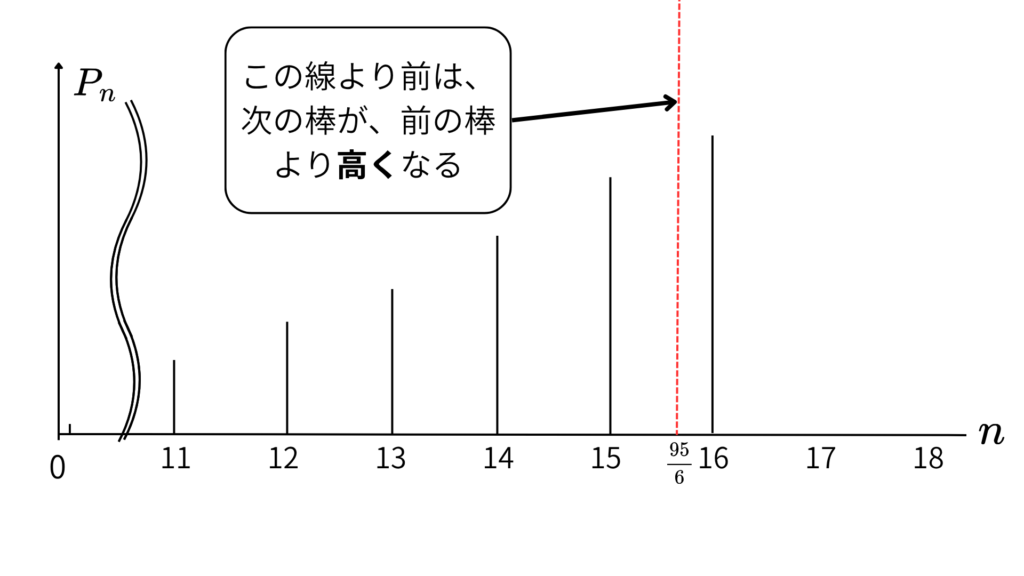
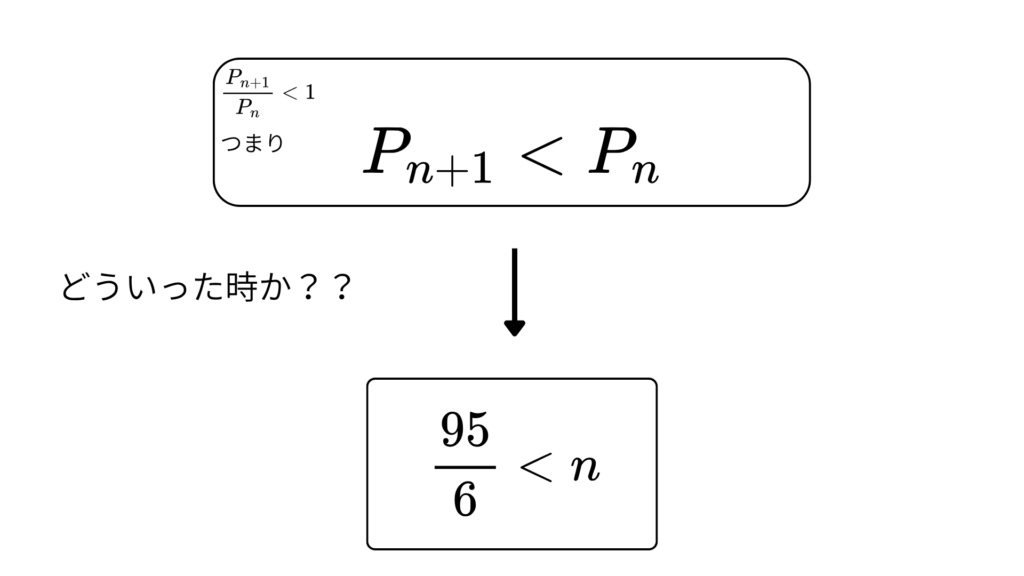
(ii)\(\;\frac{(100-n)}{5(n+1)}<1\;\)の時
(i)と不等号の向きが逆なだけなので
\(\;\frac{95}{6}<n\;\)
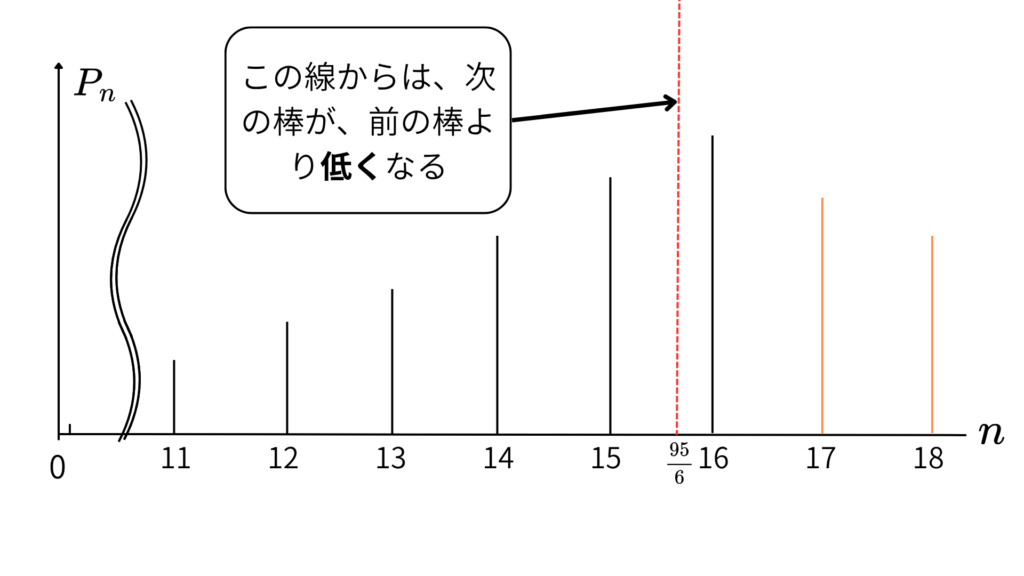
よってグラフから、
\(\;p_n\;\)が最大となる\(\;n\;\)の値は\(\;n=16\;\)
まとめ
お疲れさまでした!!
整数関数の最大最小問題は
ぱっと見は難しくなりがちです
けど、やってることは簡単なんですね
類題を解くことで応用力を身につけましょう!!
ぜひ、役立ててみてください!
まとめ記事の紹介
最大最小のまとめ
1変数多項式の最大最小まとめ

コメント