こんにちは!現役京大生のむぎといいます!
今回は、相加相乗平均の最大・最小の問題を攻略していきます!!
相加相乗平均の問題は、減点ポイントがあるのでしっかりと理解する必要があります!
この記事で得られる学び
この記事を読み切るころには次のような学びが得られているでしょう!
- 減点ポイント
- その対策
最大最小問題のどこを学ぶの?
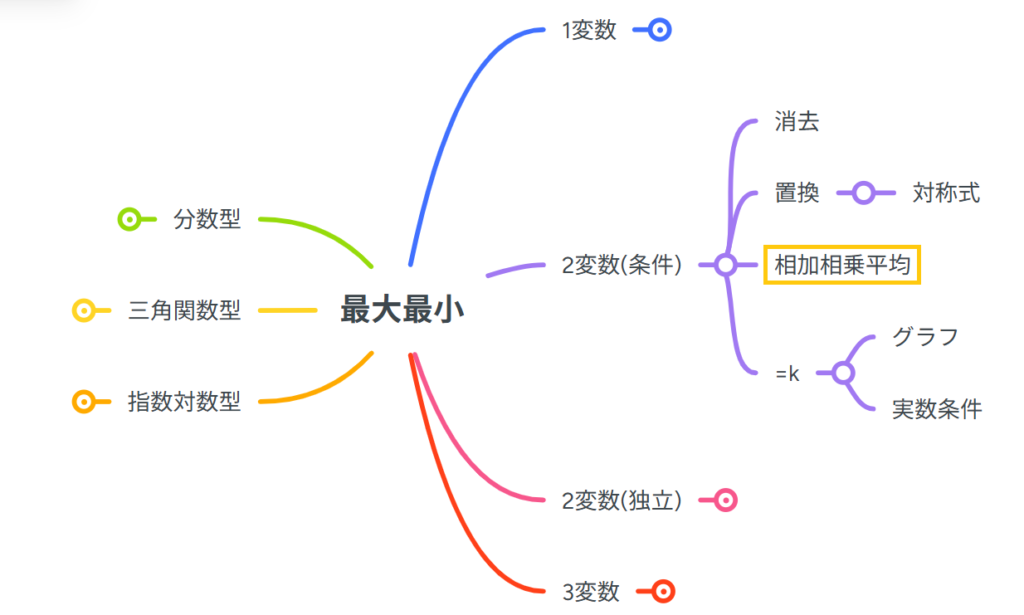
相加相乗平均の問題の全体での位置です!
全体像を知りたい人はこちらのリンクからどうぞ!
相加相乗平均とは?
このような、不等式のことです!
例題
今回の例題です
\(\;s \geq 0,t \geq 0\;\)のとき\[\;(s+\frac{2}{t})(t+\frac{8}{s})\;\]の最小値を求めよ。
重要度と難易度
| 重要度 | ★★★☆☆(3) |
| 難易度 | ★★☆☆☆(2) |
相加相乗平均はたまに出てきます重要度は普通です
思いつくのが難しさの8割みたいなところあるので、そんなむずくないです!
出題されたら確実に点が取れるよう、対策を学びましょう!!
解法ステップ
相加相乗平均の解法ステップを解説します!
- 変数が0より大きいか確認
↓ - 相加相乗平均の関係から、不等式を作る!
↓ - 等号成立条件を書く

1つ1つ解説していくね
1.変数が0より大きいか確認
\(\;s \geq 0,t \geq 0\;\)のとき\[\;(s+\frac{2}{t})(t+\frac{8}{s})\;\]の最小値を求めよ。
相加相乗平均の関係で\(\;a,b\;\)にあたる変数が0より大きいかを確認します!
というのも
この前提があるからです!
逆にこれが成り立っているときは、相加相乗平均が解法であることが多いです
今回の問題ではどうでしょう?
ぱっと見、どこが\(\;a,b\;\)にあたる変数か、わかりませんね
一度展開してみましょう
\[\;(s+\frac{2}{t})(t+\frac{8}{s})\;\]
\[=\;st+8+2+\frac{16}{st}\;\]
変数\(\;a,b\;\)を見定める1つの目安としては、逆数の和とかがあります
今回の問題も、逆数の和がありますね!
\(\;st\;\)と\(\;\frac{16}{st}\;\)です
そこが\(\;a,b\;\)にあたる変数です!
実際、今回は\(\;s \geq 0,t \geq 0\;\)であるので
\(\;st \geq 0,\frac{16}{st} \geq 0\;\)です!
これは、減点を防ぐために明記しておきましょう!
2.相加相乗平均の関係から、不等式を作る!
相加相乗平均の関係をそのまま適用します!
\[=\;10+st+\frac{16}{st} \geq 10+2\sqrt{st \cdot \frac{16}{st}}\;\]
\[\geq 10+2\sqrt{16}=18\;\]
3. 等号成立条件を書く
通常、最大値、最小値をとるときの変数の値については、
問題文に書いていない限り、書く必要はないですが(書いたほうが親切)
不等式の関係を使った最大最小は必要になります!
なんで必要??
今回の問題を使った例を見ておきましょう
2つの解法を書きます
どちらが正しいでしょうか?
\(\;s \geq 0,t \geq 0\;\)のとき\[\;(s+\frac{2}{t})(t+\frac{8}{s})\;\]の最小値を求めよ。
【解法1】
\[\;(\underline{s+\frac{2}{t}})(t+\frac{8}{s})\;\]
下線部に相加相乗平均を適用して、
\[\geq \;(2\sqrt{s \cdot \frac{2}{t}})(\underline{t+\frac{8}{s}})\; \cdots \cdots(1)\]
再び下線部に相加相乗平均を使って
\[\geq \;(2\sqrt{s \cdot \frac{2}{t}})(2\sqrt{t \cdot \frac{8}{s}})\; \cdots \cdots(2)\]
\[= \;4\sqrt{s \cdot \frac{2}{t} \cdot t \cdot \frac{8}{s}})\;\]
\[= \;4 \cdot 4=16\]
最小値は16
【解法2】
\[\;(s+\frac{2}{t})(t+\frac{8}{s})\;\]
\[=\;st+8+2+\frac{16}{st}\;\]
\[=\;10+st+\frac{16}{st} \geq 10+2\sqrt{st \cdot \frac{16}{st}}\;\]
\[\geq 10+2\sqrt{16}=18\;\]
最小値は18
正解は解法2の方です!
どうして答えが違ったのでしょう?
【解法1】で本当に16をとるのか
等号成立を確認してみましょう!
(1)の等号を満たすのは
\[\;s=\frac{2}{t}\;\]
のとき
つまり\(\;st=2\;\)のとき
また(2)の等号を満たすのは
\[\;t=\frac{8}{s}\;\]
のとき
つまり\(\;st=8\;\)のとき
もちろん\(\;st=2\;\)と\(\;st=8\;\)を両立することはできません
つまり同時に等号を満たすことができないんですね
また、不等式と最大値、最小値は別物です
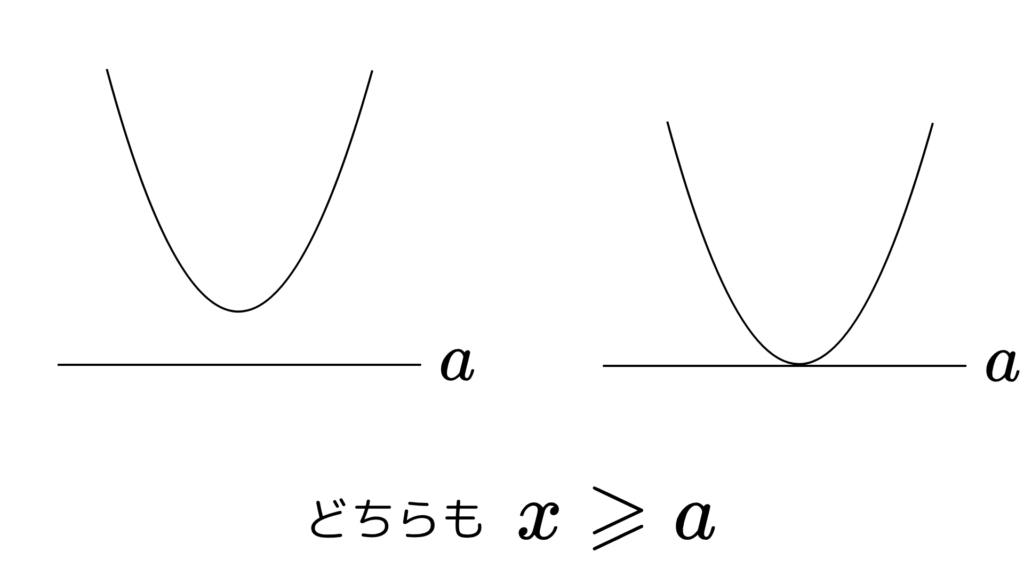
どちらも同じ、\(\;x \geq a\;\)ですが
右は最小値\(\;a\;\)となりますが、左は最小値\(\;a\;\)とはなりません!
右は\(\;x=a\;\)という保証、つまり等号成立条件があるんです。
解答
\(\;s \geq 0,t \geq 0\;\)のとき\[\;(s+\frac{2}{t})(t+\frac{8}{s})\;\]の最小値を求めよ。
\[\;(s+\frac{2}{t})(t+\frac{8}{s})\;\]
\[=\;st+8+2+\frac{16}{st}\;\]
\(\;st \geq 0,\frac{16}{st} \geq 0\;\)
相加相乗平均の関係から
\[=\;10+st+\frac{16}{st} \geq 10+2\sqrt{st \cdot \frac{16}{st}}\;\]
\[\geq 10+2\sqrt{16}=18\;\]
等号成立条件は
\[\;st=\frac{16}{st}\;\]
\(\;st \geq 0\;\)であることに注意すると
\[\;(st)^2=16\;\]
\[\;st=4\;\]
これは、例えば\(\;s=2,t=2\;\)のとき成り立つ
よって最小値は\(\;st=4\;\)のとき18
類題
類題を出します!ちょっとむずめ!
これらの問題が解けたら、相加相乗平均の最大最小の問題はばっちり!!
自信がなければもう一度Stepを見直そう!
<類題>
(1)\(\;x,y\;\)は正の実数とする。
\(\;9x^2+16y^2=144\;\)のとき、\(\;xy\;\)の最大値を求めよ
(2)\(\;x>1\;\)のとき
\(\;4x^2+\frac{1}{(x+1)(x-1)}\;\)の最小値を求めよ
解説はこちらから
まとめ
ここまで読んだあなたは、相加相乗平均の最大最小問題の解法ステップが説明できますか?
- 変数が0より大きいか確認
↓ - 相加相乗平均の関係から、不等式を作る!
↓ - 等号成立条件を書く
こうでしたね!
次相加相乗平均の最大最小の問題を見たときは一瞬で解いちゃってください!!
まとめ記事の紹介
最大最小のまとめ
【条件式】2変数関数の最大最小まとめ

コメント