こんにちは!現役京大生のむぎといいます!
最大最小問題に対してこんな悩みはありませんか?
そんな受験生にこそ、このページを読んでほしい。
最大最小問題は“型”で解ける問題なんです。
このような問題を抱えている受験生のために、
これらを「全て」フローチャートで解決します。
このシリーズで得られること

MARCH・地方国公立に完全対応
丁寧にわかりやすく説明します!!
最大最小問題のフローチャート!
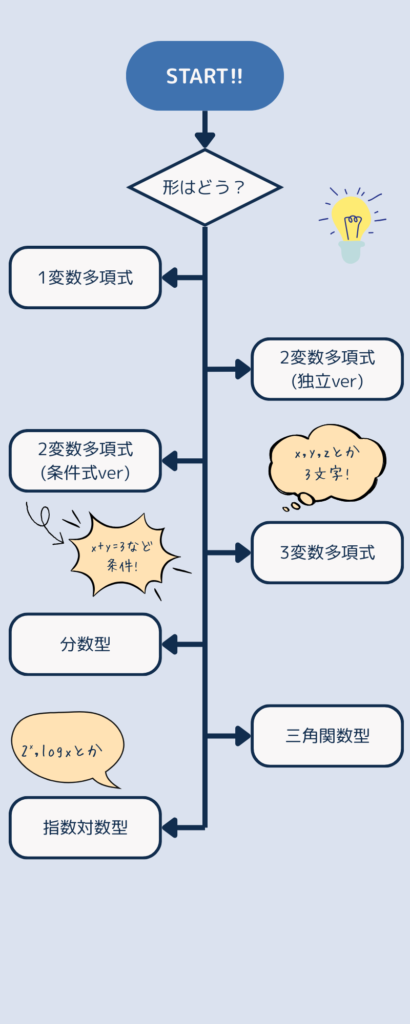
何、何っ!?いきなりめっちゃむずそうじゃん!!
って思った方も安心してください(笑)
そんなに難しいことはないので
一つ一つ、丁寧に、解説していきます!
まず、何をやっているの?
いきなり、形はどう?とか軽いノリで始まって、2変数多項式とか、意味不明ですよね(笑)
これが「何をしているか?」というと
大まかな分類をしています!
これらの最小値を求めよ。
\(x^2+3x+4\)
\(x^2-2xy+y^2-4y+6\)
これらでは解き方がかなり変わってきます
そのため、初めにある程度分類する必要があります!
つまり!問題を解く時の流れはこのようになります!!
- 最大最小問題だ!!
↓ - なんの型だろう?
↓ - 問題の“見た目”をヒントに分類
↓ - 各型のフローチャートに沿って解いていく

今からは具体的に
問題の“見た目”のヒントを紹介するね!
1変数多項式とは?
1変数多項式とは、文字の通り
“1変数“の“多項式“です
具体例では
\(x^2+3x+4\) , \(x^3+5x\) など
1変数とは、例えば \(x\) だけで構成されている式です
1つの種類の変数の文字であることがポイントです
また、多項式とは、「2つ以上の単項式の和であらわされた式」のことです
単項式とは、数字や定数 (2とか\(a\)とか) と変数 (\(x\)とか\(y\))とかを掛け合わせたものです
つまり分数の形でないということです
よって、簡単にまとめるならこのようになります
変数\(x\)とか\(y\)が
一種類 + 分母にいない
2変数多項式(独立ver,条件式ver)とは?
2変数多項式については大丈夫だと思います!
先ほどやった1変数多項式の変数が2つになったものです
ってなる人も多いと思います
これは、条件式verと一緒に考えるとわかりやすいと思います
例えば
\(x^2+4xy+2y^2+4x+7y+6\)の最小値を求めよ
この問題は何の条件式もなく\(x\),\(y\)は互いに独立しているため独立verとなります
しかしこれが
\(x+y=2\) のとき
\(x^2+4xy+2y^2+4x+7y+6\)の最小値を求めよ
このような問題では
\(x\)と\(y\)に条件式があり、\(x+y=2\)とならなければいけないので\(x\)と\(y\)は自由に動けません
よってこの問題は条件式verとなります
3変数多項式とは?
3変数多項式は今まで通り
3変数の多項式です
\(x^2+y^2+z^2=1\)のとき
\(xyz\)の最大値を求めよ
などです
分数型とは?
分数型は
\(x>0\)とする
\(\displaystyle \frac{x^2}{x^3+4x}\)の最大値を求めよ
などです!

そのまんまだね!
三角関数型
三角関数は\(\sin \theta,\cos \theta,\tan \theta\)などを使ったもので
\(\sin^2 \theta+3\cos \theta+4\)の最大値を求めよ
などです!

これもそのまんま!
指数対数型
指数対数型は\(a^x\)や\(\log\)などを使ったもので
\(4^x-2^x+3\)の最小値を求めよ
などです!
分野別リンク一覧
| 分類 | 例 | リンク |
| 1変数多項式 | \(x^2+3x+4\) , \(x^3+5x\) | 1変数多項式の最大最小 |
| 2変数多項式(独立ver) | \(x^2+4xy+2y^2+4x+7y+6\) | 2変数多項式(独立ver)の最大最小 |
| 2変数多項式(条件ver) | \(x+y=2\) のとき \(x^2+4xy+2y^2+4x+7y+6\) | 2変数多項式(条件ver)の最大最小 |
| 3変数多項式 | \(xyz\) | 3変数多項式の最大最小 |
| 分数型 | \(\displaystyle \frac{x^2}{x^3+4x}\) | 分数型の最大最小 |
| 三角関数型 | \(\sin^2 \theta+3\cos \theta+4\) | 三角関数型の最大最小 |
| 指数対数型 | \(4^x-2^x+3\) | 指数対数型の最大最小 |
あなたの苦手な最大・最小問題はどれ?
気になる項目をクリックして、すぐに攻略を始めよう!

コメント