こんにちは!現役京大生のむぎといいます!
皆さん最大最小問題に次のような悩みを抱えてないですか?
でも大丈夫です!!最大・最小問題は「型」で解けてしまいます!!
この記事で得られるもの
- 1変数多項式の最大最小問題の、解法フローチャート
- 自信を持ち迷わず解き進める力
- 安定的な得点力
- ほぼすべての解法パターン
全体像を見てみよう!

今回は、画像の黄色い線で囲まれたところを勉強するよ!!
最大最小のまとめ記事をまだご覧になっていない方は、ぜひご覧ください!!

早速、フローチャートを見ていくよ!!
【1変数多項式の最大最小】解法フローチャート
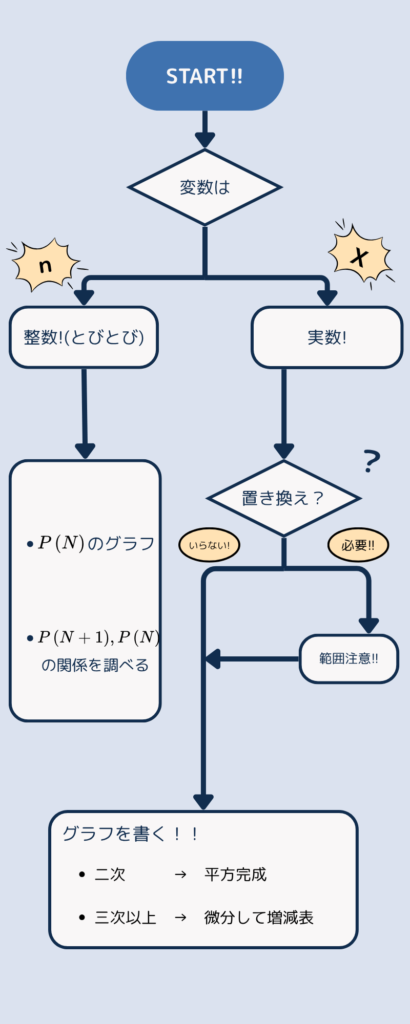

このフローチャートを保存して、いつでも見返せるようにしよう!
フローチャートの各ステップを深掘り!
実際に、フローチャートでの解法を解説します!
ただし、ここではまとめるととても長くなってしまうので、大まかな説明をします。
解法の詳しい説明については、貼られているリンクからお願いします!!
1.実数と整数
まず、実数か整数かを分類します
実数は、数直線上にある数字の集まりで、連続しており
整数は、デジタルなもので、とびとびになっています
実際には、ほとんどが実数になります。
なので、いつもは特に考えず、整数が来た時だけ
と反応できるようにしましょう!
ちなみに、整数のパターンは主に「確率の最大最小」の問題で出てきます
2.実数のとき
ここからは、実数のときの流れを説明します!

すべての基本でよく出るよ!!
頑張って学習しよう!!
置き換えが必要??
関数によっては、置き換えることで元の式よりも簡単に解けることがあります
まずは、ここにアンテナを張っておきましょう!
例えば、以下の問題
このような問題が出たとき、4次関数だから、平方完成は無理だなぁと考えて、微分!
このようにしては時間がかかったり、計算ミスをしたりしてしまいます。
\(x^2 = t\)
と置いて、
という問題に変えることで、平方完成で最小値を求めることができます
置き換えの問題のステップごとの解法のまとめや、注意点を解説した記事を貼っておきます!
ぜひ見てみてください!
グラフを書く
置き換えできるか検討をしたら、最後にグラフを書きます!!
1変数多項式のほとんどがこの“グラフを書く”で解決します!
また、2次関数のときは平方完成
3次以上の関数のときは微分をする
ということを、覚えておきましょう!!
応用問題になると難しくなる、グラフを使った最大最小問題はこちらから
3.整数のとき
整数のときは、整数関数の最大最小問題となり
確率の最大最小、数列の和の最大最小などがあります。
比較的難易度は高いですが、慣れてしまえば簡単です
主な解法は2パターンだけですので、ぜひマスターしましょう!
まとめ!
1変数多項式の最大最小はどうでしたでしょうか??
以外にも解法は少なかったのではないでしょうか?
今回紹介した解法をマスターすれば、1変数多項式の最大最小は完璧になります!!
この分野の最大最小については、もう怖いものはありません!
基本の1変数多項式を完全な得点源にしましょう!

コメント