こんにちは!現役京大生のむぎといいます!
今回は、実数条件を使う最大・最小の問題を攻略していきます!!
このタイプの解法は、線形計画法が使えなかったときに重宝されます!
2変数関数の最大最小ではよく出てくるのでマスターしましょう!!
この記事で得られる学び
この記事を読み切るころには次のような学びが得られているでしょう!
- 実数条件を使う最大最小問題の解法
- 線形計画法との使い分け
最大最小問題のどこを学ぶの?
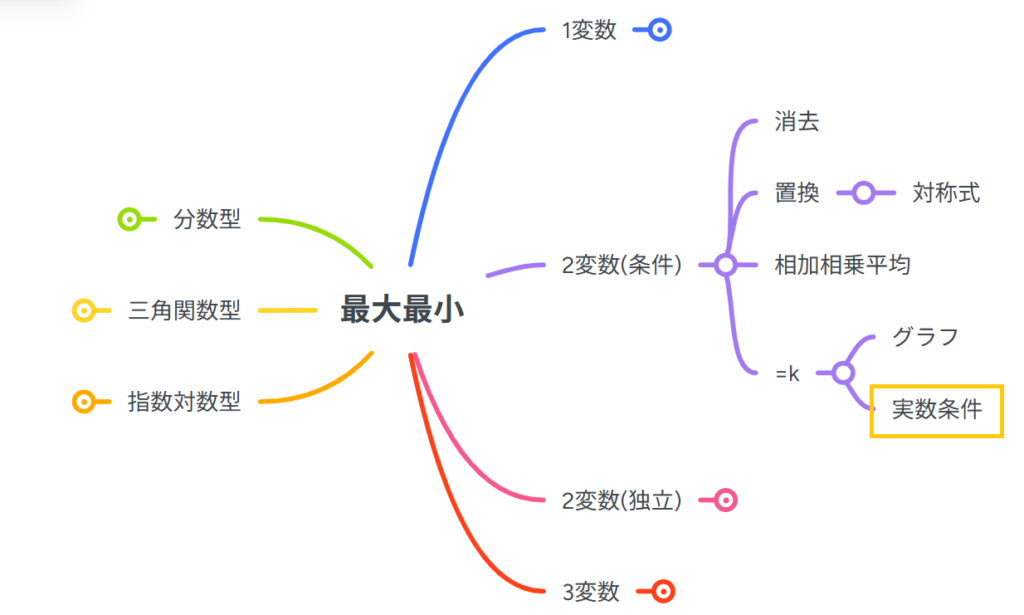
全体での位置です!
全体像を知りたい人はこちらのリンクからどうぞ!
例題
今回の例題です
実数\(\;x,y\;\)が、\(\;x^2+y^2=2x\;\)のとき、\(\;x+y\;\)の最大値および最小値を求めよ。
重要度と難易度
| 重要度 | ★★★☆☆(3) |
| 難易度 | ★★★☆☆(3) |
重要度は普通です
ちょっと難しいので、ライバルと差をつけるため、
出題されたら確実に点が取れるよう、対策を学びましょう!!
解法ステップ
解法ステップを解説します!
- 最大最小を求める\(\;f(x,y)\;\)を\(\;=k\;\)(実数)とする
↓ - 1文字消去する
↓ - \(\;x,y\;\)が実数であるような\(\;k\;\)の範囲を調べる

1つ1つ解説していくね
1.\(\;f(x,y)\;\)を\(\;=k\;\)(実数)とする
\(\;x,y\;\)が、\(\;x^2+y^2=2x\;\)のとき、\(\;x+y\;\)の最大値および最小値を求めよ。
最大最小を求める関数を\(\;k\;\)と置きます
\(\;x+y=k\;\)
2.1文字消去する
\(\;x+y=k\;\)
この式を用いてもとの式の\(\;x\;\)か\(\;y\;\)を消去します!
今回は\(\;x\;\)を消去するのには2回も代入が必要で面倒なので、
\(\;y\;\)を消去します!
\(\;y=-x+k\;\)より
\(\;x^2+y^2=2x\;\)
↓
\(\;x^2+(-x+k)^2=2x\;\)
\(\;2x^2+-2kx+k^2=2x\;\)
\(\;2x^2+-2(k+1)x+k^2=0\;\)
3. \(\;x,y\;\)が実数であるような\(\;k\;\)の範囲を調べる
最後です!!
\(\;x,y\;\)は実数であるという条件を使います
\(\;2x^2+-2(k+1)x+k^2=0\;\)から
判別式\(\;D\geq0\;\)であるので
\[\;\frac{D}{4}=(k+1)^2-2k^2\geq0\;\]
\[\;k^2-2k-1\leq0\;\]
よって、\(\;1-\sqrt{2} \leq k \leq 1+\sqrt{2}\;\)
最大値\(\;1+\sqrt{2}\;\)、最小値\(\;1-\sqrt{2}\;\)
線形計画法との使い分け
2変数の問題で最終手段となるのが
線形計画法とこのタイプの問題です
この答えは
となります!
今回の問題を線形計画法で解こうと思うと
\[\;x^2+y^2=2x\;\]
これを図示する必要があります!
無理ですよね…
なので実数条件を使うわけです!!
類題
類題を出します!
これらの問題が解けたら、実数条件を使う最大最小の問題はばっちり!!
自信がなければもう一度Stepを見直そう!
<類題>
\(\;x,y\;\)は実数とする。
\(\;x^2-2xy+2y^2=2\;\)のとき、\(\;2x+y\;\)の最大値、最小値を求めよ
解説はこちらから
まとめ
ここまで読んだあなたは、実数条件を使う最大最小の問題の解法が説明できますか?
- 最大最小を求める\(\;f(x,y)\;\)を\(\;=k\;\)(実数)とする
↓ - 1文字消去する
↓ - \(\;x,y\;\)が実数であるような\(\;k\;\)の範囲を調べる
こうでしたね!
次実数条件を使う最大最小の問題を見たときは一瞬で解いちゃってください!!
まとめ記事の紹介
最大最小のまとめ
【条件式】2変数関数の最大最小まとめ

コメント