こんにちは!現役京大生のむぎといいます!
今回は、対称式の最大・最小の問題を攻略していきます!!
対称式の問題は、
このような理由から、とても重要なテーマです!
この記事で得られる学び
この記事を読み切るころには次のような学びが得られているでしょう!
- そもそも、対称式って何?
- 対称式の最大最小問題の基本的な解き方
- 減点ポイント
最大最小問題のどこを学ぶの?
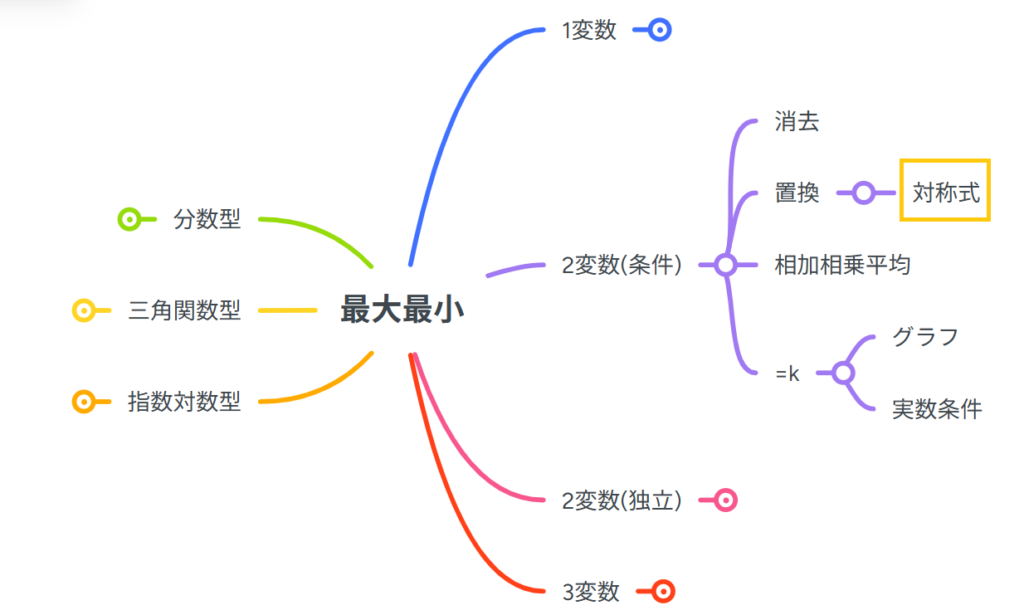
対称式の問題の全体での位置です!
全体像を知りたい人はこちらのリンクからどうぞ!
そもそも対称式って何?
対称性があるとは
文字を入れ替えても式が変わらない状態のことです
例えば、
\(\;x^2+4x+2xy+4y+y^2\;\)
\(\;(3x+y)^2+(3y+x)^2\;\)
などです!
(実際に\(\;x\;\)と\(\;y\;\)を入れ替えてみると、式が変わらないことがわかります)
例題
今回の例題です
\(\;x,y\;\)を実数とする。\(x^2+xy+y^2=3\;\)のとき
\(x^2+y^2+2(x+y)\;\)の最大値、最小値を求めよ。
重要度と難易度
| 重要度 | ★★☆☆☆(2) |
| 難易度 | ★★★★☆(4) |
あんまり出てこないので重要度は低いです。
しかし、難しく思う人も多いと思うので、これが解ければ大きなアドバンテージになります!!
ぜひここで、マスターしましょう!!
解法ステップ
対称式の解法ステップを解説します!
- \(x+y=s\;\)
\(xy=t\;\)とする
↓ - \(\;s^2-4t \geq 0\;\)の条件を足す
↓ - 置き換えた式の最大最小を求める

1つ1つ解説していくね
1.x+y=s,xy=t とする
\(\;x,y\;\)を実数とする。\(x^2+xy+y^2=3\;\)のとき
\(x^2+y^2+2(x+y)\;\)の最大値、最小値を求めよ。(例題再掲)
対称式の性質として
というものがあります!
だから、\(\;x+y=s\;\),\(\;xy=t\;\)とすると
\(\;x,y\;\)の式が\(\;s,t\;\)の式で表すことができます!!
\(\;x+y=s\;\),\(\;xy=t\;\)とすると
\(x^2+xy+y^2=3\;\) → \(\;s^2-t=3\;\)
また求める最大最小は
\(x^2+y^2+2(x+y)\;\)の最大最小 → \(s^2-2t+2s\;\)の最大最小
2.\(\;s^2-4t \geq 0\;\)の条件を足す
ここが、対称式の問題を解く時の、1番の注意点です!!
\(\;s^2-4t \geq 0\;\)
この、隠れた条件が足されます
なんでこの条件が付く?
この条件がない状況を考えてみましょう!
先ほど、\(\;x,y\;\)の式が\(\;s,t\;\)の式になったので
\(\;s^2-t=3\;\)のとき
\(s^2-2t+2s\;\)の最大最小を求めよ
という問題になりました。
この問題を解いてみましょう!!
フローチャートをたどると
最大最小→2変数関数(条件式)→消去できる
となります!
続けていくと
\(\;s^2-t=3\;\)より
\(\;t=s^2-3\;\)として\(\;t\;\)を消去する。
\(s^2-2t+2s\;\) → \(s^2-2(s^2-3)+2s\;\)
つまり、
\(-s^2+2s+6\;\)の最大最小を求める。
これで1変数多項式の最大最小になりました!
さらに続けていくと
実数→置き換えいらない→グラフから求める
\(-s^2+2s+6\;\)の最大最小を求める。
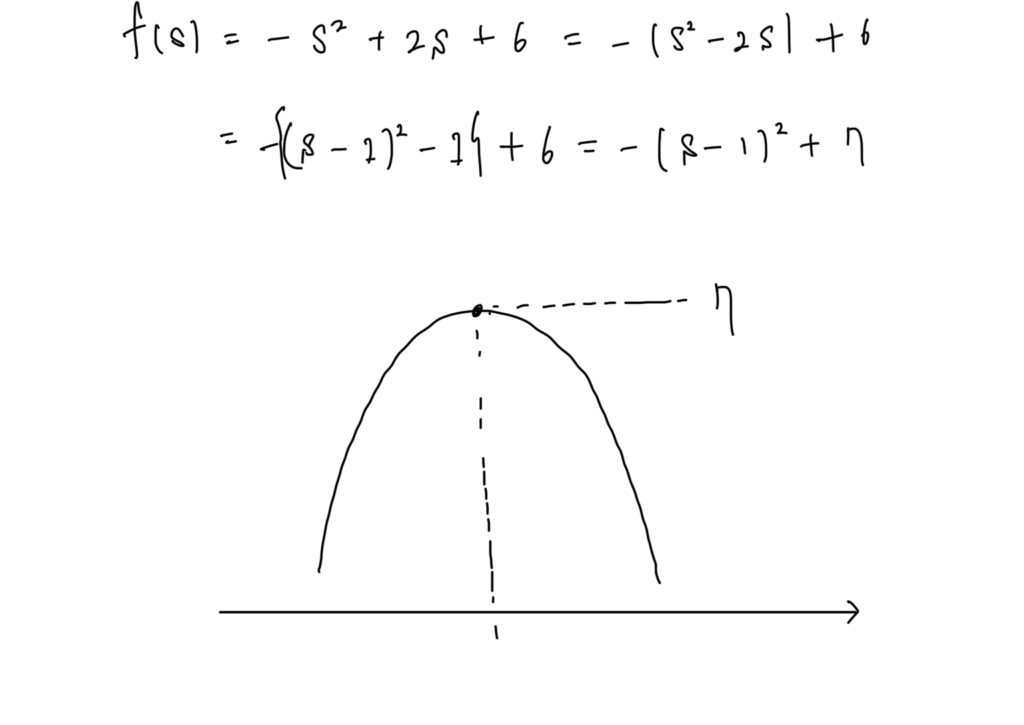
よって、グラフから
最大値は7
最小値はなし
このようになりました。
一見何の問題もないですが、1つ間違っているところがあります
それが、
実数\(\;x,y\;\)が存在しないことがある
ということです
例えば、今回は\(\;s\;\)の範囲は実数全体としていますが
\(\;s=3\;\)のとき
\(\;t=s^2-3\;\)より
\(\;t=6\;\)
このときの\(\;x,y\;\)を求めてみましょう!!
どうやって求めるかわかりますか??
知らないと難しいと思いますが、解と係数の関係を使います
解と係数の関係
2次方程式\(\; ax^2-bx+c=0\;\) の解を、\(\;\alpha, \beta\;\) とすると、
- \(\; \alpha + \beta = \frac{b}{a}\;\)(和)
- \(\; \alpha \beta = \frac{c}{a}\;\)(積)
これを逆向きに利用します!
つまり!
解と係数の関係の逆
- \(\; \alpha + \beta = \frac{b}{a}\;\)(和)
- \(\; \alpha \beta = \frac{c}{a}\;\)(積)とすると
\(\;\alpha,\beta\;\)は2次方程式\(\; ax^2-bx+c=0\;\) の2解である
ここで\(\;a=1\;\)とすれば
解と係数の関係の逆
- \(\; \alpha + \beta = b\)(和)
- \(\; \alpha \beta = c \)(積)とすると
\(\;\alpha,\beta\;\)は2次方程式\(\; x^2-bx+c=0\;\) の2解である
となります!
今回の問題に応用するために
\(\;\alpha,\beta\;\)→\(\;x,y\;\)
\(\;b\;\)→\(\;s\;\)
\(\;c\;\)→\(\;t\;\)
\(\;x\;\)の方程式→\(\;u\;\)の方程式とします!
すると、
- \(\; x + y = s \;\)(和)
- \(\; xy = t \;\)(積)とすると
\(\;x,y\;\)は2次方程式\(\; u^2-su+t=0\;\) の2解である
となります!
\(\;s=3\;\),\(\;t=6\;\)であるので
\(\;x,y\;\)は2次方程式\(\; u^2-3u+6=0\;\) の2解である
となります!
よって、解の公式から求めると
\[\;(x,y)\;=(\frac{3+ \sqrt{15}i}{2},\frac{3- \sqrt{15}i}{2})\]
全然実数じゃありませんね
つまり、\(\;s,t\;\)が実数だとしても、\(\;x,y\;\)が実数ではないので、
\(\;x,y\;\)が実数という条件からずれてしまうということです
図で表すとこんな感じです
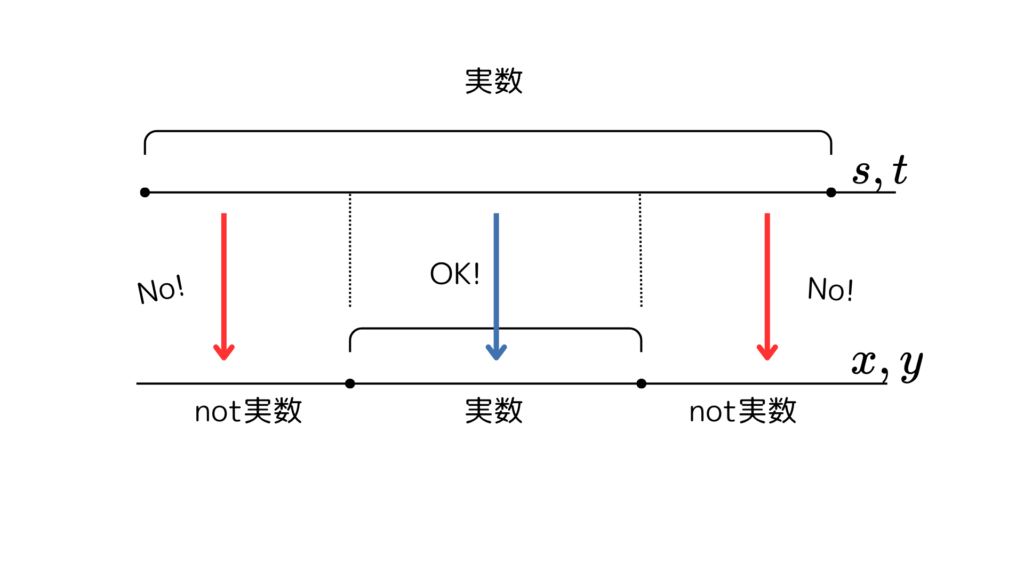
じゃあどうしたらいいのか?というと
\(\;x,y\;\)が実数であるように\(\;s,t\;\)の範囲を狭めればいいわけです!
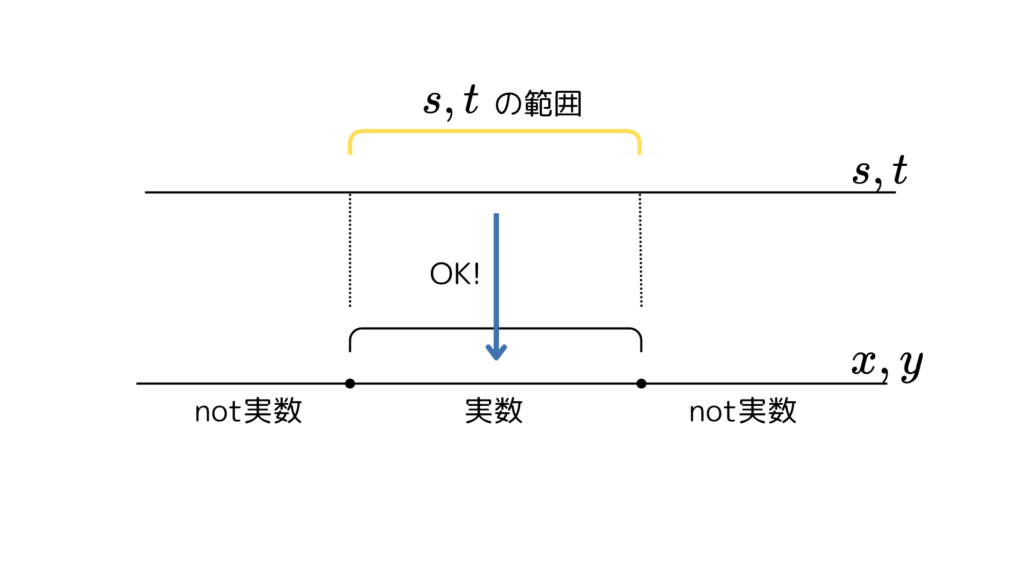
こういうことですね!
置き換えを使う最大最小でも言いましたが
置き換えをするときは範囲に注意しないといけないんです!!
これもその一例ですね!
要するに\(\;x,y\;\)が実数であるようにすればいいんですよね?
\(\;x,y\;\)が何だったか?というと、
\(\;x,y\;\)は2次方程式\(\; u^2-su+t=0\;\) の2解である
というのがありましたね!
方程式の解\(\;x,y\;\)が実数である….
判別式!!ですね
つまり
\[\;D=s^2-4t \geq 0\;\]
という条件が付くわけですね!
難しい話だったと思いますが、
しっかりと理解しておきましょう!!
\(\;s,t\;\)と置き換えたら範囲に注意!!
\[\;s^2-4t \geq 0\;\]
3.置き換えた式の最大最小を求める
ここまで来たら、あとは2変数関数の最大最小のフローチャートをたどれば解くことができます!
復習として今回の例題を、最初から解いてみます!
\(\;x,y\;\)を実数とする。\(x^2+xy+y^2=3\;\)のとき
\(x^2+y^2+2(x+y)\;\)の最大値、最小値を求めよ。(例題再掲)
- 対称式だから
\(\;x+y=s\;\),\(\;xy=t\;\)とすると
\(x^2+xy+y^2=3\;\) → \(\;s^2-t=3\;\)
また求める最大最小は
\(x^2+y^2+2(x+y)\;\)の最大最小 → \(s^2-2t+2s\;\)の最大最小 - 解と係数の関係より、\(\;x,y\;\)は2次方程式\(\; u^2-su+t=0\;\) の2解である
\(\;x,y\;\)は実数であるので、
\[\;D=s^2-4t \geq 0\;\] - ここからは、再び、条件式付き2変数関数の最大最小のフローチャート通りにやる!!
文字消去できる?
↓
できる!!
文字消去の解法でやる!
a.文字消去をする!
\(\;s^2-t=3\;\)から、\(\;t=s^2-3\;\)
これを用いて\(\;t\;\)を消去すると
求める最大最小は
\(s^2-2(s^2-3)+2s\;\)の最大最小となる
b.範囲に注意する!
\(\;t\;\)を消去したから、\(\;t\;\)の範囲に注意!
\[\;s^2 \geq 4t\;\]
に、\(\;t=s^2-3\;\)を代入すると
\[\;s^2 \geq 4(s^2-3) \;\]
\[\;12 \geq 3s^2 \;\]
\[\;4 \geq s^2 \;\]
\[\; -2 \leq s^2 \leq 2\;\]
c.1変数多項式の最大最小を求める

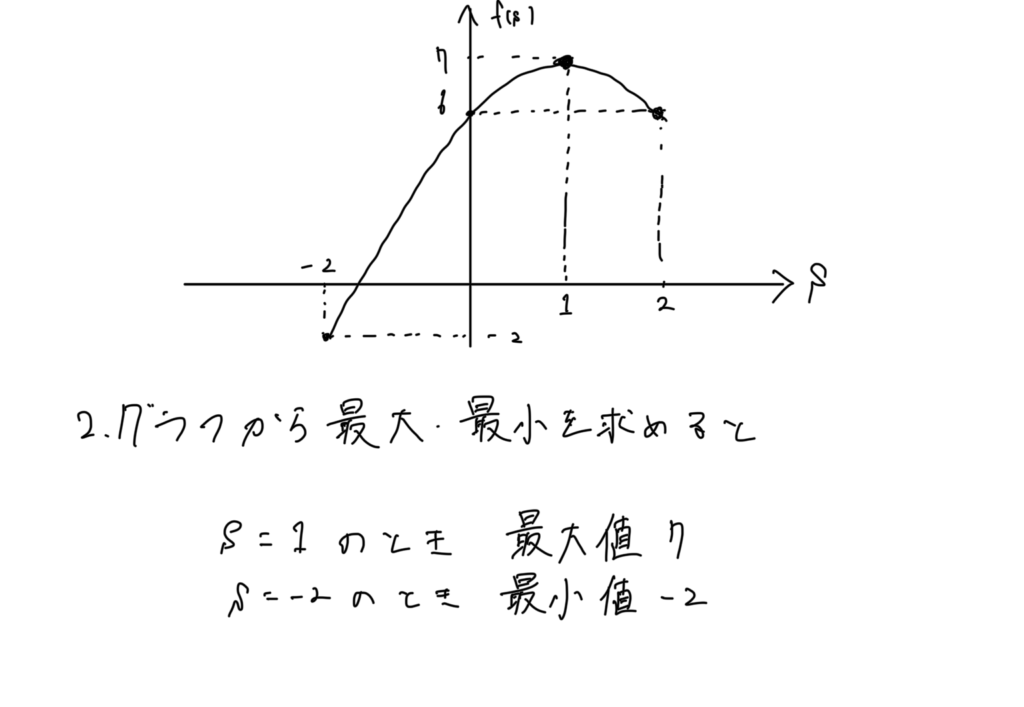
こんな感じで、難しそうに見える問題も
結局簡単な解法の組み合わせなんですね!!
類題
類題を出します!(難しいかも!)
これらの問題が解けたら、対称式の最大・最小の問題はばっちり!!
自信がなければもう一度Stepを見直そう!
<類題>
\(\;x,y\;\)を実数とする。
x^2+xy+y^2=6のとき
次の関数の最大、最小を求めよ
\(\;x^2y+xy^2-x^2-2xy-y^2+x+y\;\)
解説はこちらから
まとめ
ここまで読んだあなたは、対称式の最大最小問題の解法ステップが説明できますか?
- \(x+y=s\;\)
\(xy=t\;\)とする
↓ - \(\;s^2-4t \geq 0\;\)の条件を足す
↓ - 置き換えた式の最大最小を求める
こうでしたね!
次対称式の問題を見たときは一瞬で解いちゃってください!!
まとめ記事の紹介
最大最小のまとめ
【条件式】2変数関数の最大最小まとめ

コメント